Canons rythmiques

Canons rythmiques

Canon rythmique

Sommaire

Définition, historique

La notion de canon est ancienne en musique. L'étude spécifique de la théorie des canons rythmiques, qui se focalise sur les seuls rythmes en ignorant hauteurs, timbres et autres paramètres du son, a été vraiment initiée par Dan Tudor Vuza dans les années 1980. Le principe du canon est simple, plusieurs voix jouent un même motif mais décalé dans le temps. Pour un canon rythmique on peut formaliser une voix par la suite des instants où une note est jouée, A = (a1,a2...an). On a affaire à un canon si toutes les voix sont translatées l'une de l'autre: A' = (a'1,a'2...a'n) = A + b. Si on note B = (b1,b2...bn) l'ensemble des décalages, les différentes voix sont les bi + (a1,a2...an).

Bien entendu on peut faire des canons rythmiques sans autre contrainte; le problème devient intéressant quand on exige que les voix ne se recouvrent pas, i.e. que la somme A + B soit directe, i.e. encore qu'il n'y ait pas plus d'une note par instant. C'est encore plus contraignant si on exige exactement une note, ni plus ni moins, par instant. On retrouve alors un problème de pavage (ou mosaïque).

Différents théorèmes techniques établissent qu'un canon qui pave tous les instants possibles avec un motif fini est nécessairement périodique, et qu'un canon possède nécessairement une unité de temps commune. 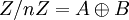On est donc ramené mathématiquement parlant à la question d'un pavage de l'ensemble Z des entiers relatifs de la forme Z = a + B + nZ ou encore, passant au quotient modulo la période n du canon, Z/n Z = A\oplus B.

Vuza s'est intéressé particulièrement aux cas où ni A, ni B ne possèdent de période propre, qu'il appelle RCMC (Rhythmic Canon of Maximal Category) et que les chercheurs suivants ont plutôt appelé "canons Vuza". Il s'avère que les résultats retrouvés par Vuza à ce propos sont équivalents à une difficile classification des groupes cycliques étudiée par plusieurs mathématiciens depuis les années 1950 et achevée par Sands.

Résultats mathématiques

Les vieux théorèmes : Hajos, De Bruijn.

Les bons et mauvais groupes (Sands).

Exemples.

Développements récents

Dénombrements

Fripertinger.

Lien avec la conjecture de Fuglede

Amiot

Extensions de la notion de canon rythmique

Canon par rétrogradation

Exemples. Le théorème du trichorde de Wild.

Canons par augmentation

Le problème de Johnson avec 0 1 4.

Le théorème de périodicité peut-il se généraliser ?

Canons modulo p

Leur existence inconditionnelle.

Bibliographie

  • Portail de la musique Portail de la musique
Ce document provient de « Canon rythmique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Canons rythmiques de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Canon rythmique — En musique, un canon rythmique est analogue à un canon traditionnel (superposition à elle même d une phrase musicale donnée). La seule différence est que les hauteurs des notes ne sont pas prises en compte mais seulement leur durée (seul le… …   Wikipédia en Français

  • Canon Rythmique — Sommaire 1 Définition, historique 2 Résultats mathématiques 3 Développements récents 3.1 Dénombrements …   Wikipédia en Français

  • MESSIAEN (O.) — Par son œuvre et son enseignement, Messiaen est sans doute le musicien français qui a le plus influencé la musique composée après la Seconde Guerre mondiale. Par ses recherches éloignées de tout esprit de système, il n’a rien renié de l’apport… …   Encyclopédie Universelle

  • Poèmes pour Mi — le Dauphiné, région qui inspira au musicien les Poèmes pour Mi Poèmes pour Mi est une œuvre pour grand soprano dramatique et orchestre d Olivier Messiaen, composée dans les années 1936 37 et dédiée à la première épouse du compositeur, Claire… …   Wikipédia en Français

  • CONTREPOINT — Le contrepoint est l’art de faire chanter en toute indépendance apparente des lignes mélodiques superposées, de telle manière que leur audition simultanée laisse clairement percevoir, au sein d’un ensemble cohérent, la beauté linéaire et la… …   Encyclopédie Universelle

  • RYTHME (musique) — La ponctuation égale d’une goutte d’eau qui tombe; les battements du cœur, avec l’alternance continue d’un temps fort et d’un temps faible, systole et diastole; la respiration où se succèdent identiques à elles mêmes une durée brève,… …   Encyclopédie Universelle

  • CINÉMA D’ANIMATION — La représentation symbolisée, suggérée ou réalisée du mouvement apparaît comme une tentation constante des arts plastiques. Des siècles de simulacre magique, de théâtre d’ombres ou de spectacle de projection confirment la persistance du vieux… …   Encyclopédie Universelle

  • ORNEMENT (musique) — Les ornements ont existé de tout temps et dans toutes les musiques ; ils représentent un des modes les plus riches de l’expression spontanée des sentiments qui animent un interprète. Issus de l’imagination créatrice et de la sensibilité, ils… …   Encyclopédie Universelle

  • FUGUE — «La fugue (de fuga , fuite) est une forme de composition musicale dont le thème, ou sujet, passant successivement dans toutes les voix, et dans diverses tonalités, semble sans cesse fuir .» Ainsi Marcel Dupré définit il la fugue. La fugue est… …   Encyclopédie Universelle

  • Fast as a Shark — Chanson par Accept extrait de l’album Restless and Wild Sortie octobre 1982 Enregistrement février, mars et juin 1982 Dierks Studios (Cologne) Durée 3:48 Genre …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”