Bond Graph

Bond Graph

Graphe de liaisons

Un Bond Graph - également appelé Graphe à liens ou Graphe de liaisons - est une représentation graphique d'un système dynamique physique (mécanique, électrique, hydraulique, pneumatique, etc.) qui représente les transferts d'énergie dans le système. Les Bond Graphs sont basés sur le principe de la conservation de la puissance. Les liens d'un Bond Graph sont des symboles qui représentent soit des flux d'énergie, soit des flux d'information.

Le Bond Graph est un outil mathématique utilisé en ingénierie des systèmes. Il permet de modéliser un système piloté afin d'optimiser son dimensionnement et la conception de ses lois de commande.

Comparés à une autre représentation visuelle du système en schéma-bloc, les Bond Graphs ont plusieurs avantages :

  • ils distinguent les flux d'énergie des flux d'information ;
  • puisqu'ils reposent sur le principe de la conservation de l'énergie, ils rendent impossible d'insérer de l'énergie inexistante dans le système ;
  • ils mettent en évidence la causalité entre les efforts (force, tension, pression) et les flux (vitesse, courant, débit). Cette causalité est rajoutée une fois que le schéma initial a été construit, ce qui permet entre autres de détecter des phénomènes modélisés qui ne sont pas physiques tels qu'imposer un courant dans une bobine, la vitesse d'un volant d'inertie, etc. ;
  • comme chaque lien représente un flux bidirectionnel, les systèmes qui produisent des contre-efforts (exemple : force électromotrice des moteurs) qui agissent sur le système se représentent sans ajout de boucle de contre-réaction.

Si la dynamique du système à modéliser opère sur différentes échelles de temps, les comportements rapides en temps réel peuvent être modélisés comme des phénomènes instantanés en utilisant des Bond Graphs hybrides.

Sommaire

Analogie entre les différents domaines

Les Bond Graphs représentent le transfert de puissance entre éléments, donc ils conviennent parfaitement pour modéliser des systèmes qui relient plusieurs domaines de la physique tels que l'électricité et la mécanique. Mais avant de se lancer dans la modélisation, il faut définir une notion de puissance pour chacun des domaines. Il est nécessaire de définir certaines notions de physique.

  • La puissance

La puissance est le produit d'un flux par un effort.

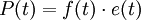
P(t)=f(t)\cdot e(t)~

  • Le moment

C'est une notion causale liée à l'effort. Ses valeurs futures sont liées à son passé par une intégration.

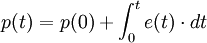
p(t)=p(0)+\int_{0}^t e(t) \cdot dt~

  • Le déplacement

C'est une notion causale liée au flux. Ses valeurs futures sont liées à son passé par une intégration.

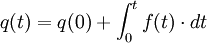
q(t)=q(0)+\int_{0}^t f(t) \cdot dt~

Grâce à ces définitions, nous allons pouvoir définir pour chaque domaine de la physique, la grandeur associée à ces définitions.

Représentation des variables pour plusieurs domaines
Domaine Effort (e) Flux (f) Moment (p) Déplacement (q)
Electrique Tension (V) Courant (A) Flux (Wb) Charge (C)
Mécanique en translation Effort (N) Vitesse (m/s) Impulsion (N.s) Déplacement (m)
Mécanique en rotation Couple (Nm) Vitesse (rad/s) Impulsion (Nm.s) Angle (rad)
Hydraulique Pression (Pa) Débit volumique (m3/s) Impulsion de pression (Pa.s) Volume (m3)
Magnétique Force magnéto-motrice (A) Dérivée flux (V) - Flux (Wb)
Chimique Potentiel Chimique (J/mol) Flux molaire (mol/s) - Quantité de matière (mol)
Thermodynamique Température (K) Flux entropique (W/K) - Entropie (J/K)
Acoustique Pression (Pa) Débit acoustique (m3/s) Impulsion de pression (Pa.s) Volume (m3)

Elements constitutifs

Les liaisons

Cet élément permet de symboliser les transferts d'énergie entre les différents processeurs. Il est représenté comme suit :

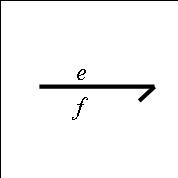Une liaison type d'un Bond Graph

On peut remarquer deux éléments sur cette liaison. La lettre e représente la composante effort de la liaison. La lettre f représente la composante flux de la liaison. La multiplication de ces deux termes doit donner la puissance qui transite par la liaison. Cet élément est orienté dans le sens où la puissance est positive.

Les sources d'effort ou de flux

Il existe deux types de sources.

  1. Les sources d'effort notées Se.
  2. Les sources de flux notées Sf.

Ces éléments fournissent une valeur constante de flux ou d'effort selon le cas quelle que soit la valeur de l'autre grandeur (Effort ou flux) fournie. De plus, ces sources peuvent avoir des discontinuités sur la grandeur qu'elles ne garantissent pas. On considère que ces sources sont parfaites, même si cela constitue une approximation par rapport au phénomène réel.

L'élément dissipatif R

L'élément dissipatif est représenté par un R. C'est un objet qui relie le flux et l'effort par une relation indépendante du temps, une fonction mathématique.

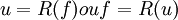
u = R(f) ou f = R(u)~

Physiquement, il correspond à un objet dissipatif. Par exemple une résistance dans le cas électrique, un frottement visqueux dans le cas mécanique.

L'élément inertiel I

Le processeur I fait apparaître entre e et f une relation temporelle via une intégration ou une dérivée. Celui-ci peut se décrire de cette façon :

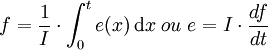
f = \frac{1}{I} \cdot \int_{0}^t e(x)\, \mathrm dx \;ou \;e = I \cdot \frac{df}{dt}

Ce processeur, qui est représenté par un I, peut être soit une inductance dans le cas électrique, soit une inertie dans le cas mécanique.

L'élément capacitif C

Le processeur C fait apparaître entre e et f une relation temporelle via une intégration ou une dérivée. Celui-ci peut se décrire de cette façon :

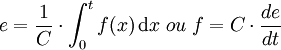
e = \frac{1}{C} \cdot \int_{0}^t f(x)\, \mathrm dx \;ou \;f = C \cdot \frac{de}{dt}

Ce processeur peut être un condensateur dans le cas électrique, un ressort dans le cas mécanique.

Il est représenté par un C.

Le transformateur

Cet élément permet la transformation des valeurs sans pertes de puissance suivant ces équations avec un rapport m :

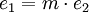
e_1 = m \cdot e_2

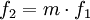
f_2 = m \cdot f_1

Cet élément est représenté par le symbole suivant : TF Dans le cas électrique, cela peut-être un transformateur ou bien un réducteur dans le cas mécanique.

Le gyrateur

Cet élément permet la transformation des valeurs sans pertes de puissance suivant ces équations avec un rapport g :

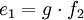
e_1 = g \cdot f_2

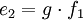
e_2 = g \cdot f_1

Cet élément est représenté par le symbole suivant : GY Dans le cas électrique, cela peut-être un gyrateur. Les moteurs sont tous des gyrateurs dans leur liaison entre la partie électrique et mécanique.

Laboratoires francophones de recherches sur la modélisation par Bond Graph

Equipes de recherche en France

Les laboratoires de recherche associés aux principaux centres d'enseignements de la modélisation Bond Graph en France sont indiqués ci-dessous :

Equipes de recherche en Suisse

Equipes de recherche en Tunisie

Bibliographie en français

Bibliographie en anglais

  • (en) Gawthrop, P. J. and Ballance, D. J., « Symbolic computation for manipulation of hierarchical bond graphs » in Symbolic Methods in Control System Analysis and Design, N. Munro (ed), IEE, London, 1999, ISBN 0-85296-943-0.
  • (en) Gawthrop, P. J. and Smith, L. P. S., Metamodelling: bond graphs and dynamic systems, Prentice Hall, 1996, ISBN 0-13-489824-9.
  • (en) Karnopp, D. C., Rosenberg, R. C. and Margolis, D. L., System dynamics: a unified approach, Wiley, 1990, ISBN 0-471-62171-4.
  • (en) Thoma, J., Bond graphs: introduction and applications, Elsevier Science, 1975, ISBN 0-08-018882-6.
  • (en) Paynter, H.M. 'An epistemic prehistory of Bond Graphs', 1992.

Liens externes

Ce document provient de « Graphe de liaisons ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Bond Graph de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Bond graph — A bond graph is a graphical description of a physical dynamic system. It is an energy based graphical technique for building mathematical models of dynamic systems. A bond graph depicts the energy flow between components used to model a system.… …   Wikipedia

  • Hybrid bond graph — A hybrid bond graph is a graphical description of a physical dynamic system with discontinuities. Similar toa regular bond graph, it is an energy based technique. However, it allows instantaneous switching of the junction structure, which may… …   Wikipedia

  • Bond — Bond, bonds, bonded, and bonding may refer to:Fiduciary bonds*Bond (finance), in finance, a debt security, issued by Issuer **Government bond, a bond issued by a national government ***Government bond register, a register of bonds issued by a… …   Wikipedia

  • Glossary of graph theory — Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with… …   Wikipedia

  • Quantum graph — In mathematics and physics, a quantum graph is a linear, network shaped structure whose time evolution is described by a system of schrödinger equations or, more generally, by a set of evolution equations associated with differential or pseudo… …   Wikipedia

  • Periodic graph (crystallography) — For other uses, see Periodic graph. A (large) unit cell of Diamond crystal net; the balls represent carbon atoms and the sticks represent covalent bonds …   Wikipedia

  • Graphe des liaisons — Graphe de liaisons Un Bond Graph également appelé Graphe à liens ou Graphe de liaisons est une représentation graphique d un système dynamique physique (mécanique, électrique, hydraulique, pneumatique, etc.) qui représente les transferts d… …   Wikipédia en Français

  • Graphe à liens — Graphe de liaisons Un Bond Graph également appelé Graphe à liens ou Graphe de liaisons est une représentation graphique d un système dynamique physique (mécanique, électrique, hydraulique, pneumatique, etc.) qui représente les transferts d… …   Wikipédia en Français

  • Graphe de liaisons — Pour les articles homonymes, voir Graphe de liaisons (homonymie). Un graphe de liaisons également appelé graphe à liens ou bond graph est une représentation graphique d un système dynamique physique (mécanique, électrique, hydraulique,… …   Wikipédia en Français

  • List of mathematics articles (H) — NOTOC H H cobordism H derivative H index H infinity methods in control theory H relation H space H theorem H tree Haag s theorem Haagerup property Haaland equation Haar measure Haar wavelet Haboush s theorem Hackenbush Hadamard code Hadamard… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”