- Trisection du carré
-
La trisection du carré consiste à découper un carré en plusieurs morceaux de manière à reconstituer par assemblage des pièces obtenues, trois carrés de surfaces identiques.
Fig.1. Une trisection du carré due à Henry Perigal (1891)
Fig. 2. Trisection du carré en 6 pièces de même surface (2010).Sommaire
Historique du problème
La dissection du carré en trois partitions congruentes est un problème de géométrie qui remonte à l'époque où la civilisation islamique et le monde arabo-musulman étaient dans son âge d'or. Les artisans qui maîtrisaient l'art du zellige avaient besoin de techniques novatrices pour réaliser leurs fabuleuses mosaïques aux figures géométriques complexes. Ainsi, la première solution à ce problème fut proposée au Xe siècle par le mathématicien perse Abu'l-Wafa' (940-998) dans son traité Sur l'indispensable aux artisans en fait de construction[1]. Abu'l-Wafa' utilisa également sa dissection pour illustrer le théorème de Pythagore[2] . Cette démonstration géométrique du théorème de Pythagore sera redécouverte dans les années 1835-1840[3] par Henry Perigal[4] et publiée en 1875[5].
Recherche d'optimalité
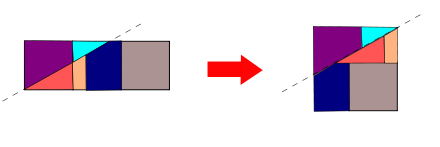
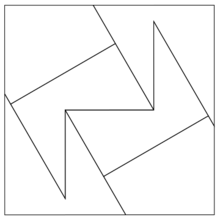
La beauté d'une dissection dépend de plusieurs paramètres. Il est cependant d'usage de rechercher les solutions comportant le minimum de pièces. Loin d'être minimale, la trisection du carré proposée par Abu'l-Wafa' utilise 9 morceaux. Au XIVe siècle, Abu Bakr al-Khalil propose deux solutions dont une en 8 morceaux[6]. Vers la fin du XVIIe, Jacques Ozanam se repenche sur le problème[7] et au XIXe siècle des solutions en 8 et 7 morceaux sont proposées, dont une par le mathématicien Édouard Lucas[8]. C'est en 1891 que Henry Perigal publie la première solution connue en 6 pièces seulement[9] (voir Fig. 1). De nos jours, de nouvelles dissections continuent d'être découvertes[10] (voir Fig. 2) et la conjecture que 6 est le nombre minimal de pièces n'est toujours pas démontrée.
Références
- (en) Alpay Özdural (1995), « Omar Khayyam, Mathematicians, and “conversazioni” with Artisans », Journal of the Society of Architectural Vol. 54, No. 1, Mar., 1995
- (en) Reza Sarhangi, Slavik Jablan (2006). Elementary Constructions of Persian Mosaics. Towson University and The Mathematical Institute. online
- (en) Voir appendice de L. J. Rogers (1897). Biography of Henry Perigal: On certain Regular Polygons in Modular Network. Proceedings London Mathematical Society. Volume s1-29, Appendix pp. 732-735.
- (en) Henry Perigal sur wikisource
- (en) Henry Perigal (1875). On Geometric Dissections and Transformations, Messenger of Mathematics, No 19, 1875.
- (en) Alpay Özdural (2000). Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World, Historia Mathematica, Volume 27, Issue 2, May 2000, Pages 171-201.
- Jean-Étienne Montucla (1778), complété et ré-édité par Jacques Ozanam (1640-1717) Récréations mathématiques, Tome 1 (1694), p. 297 Pl.15.
- Édouard Lucas (1883), Récréations Mathématiques, Volume 2. Paris, Gauthier-Villars. 2e édition (1893) ré-imprimée par Blanchard en 1960. Voir p. 151 et 152 du Volume 2 de cette édition. online (pp. 145-147).
- (en) Henry Perigal (1891). Geometric Dissections and Transpositions, Association for the Improvement of Geometrical Teaching.
- (en) Christian Blanvillain et János Pach (en) (2010). Square Trisection. Bulletin d'Informatique Approfondie et Applications N°86 - Juin 2010 également disponible à l'EPFL sur: oai:infoscience.epfl.ch:161493.
Bibliographie
- (en) Greg N. Frederickson, Dissections: Plane and Fancy, Cambridge, Cambridge University Press, 1997 (ISBN 978-0-521-57197-5) (LCCN 97011189) [lire en ligne]
- (en) Greg N. Frederickson, Hinged Dissections: Swinging and Twisting, Cambridge, Cambridge University Press, 2002 (ISBN 978-0-521-81192-7) (LCCN 2001043450) [lire en ligne]
- (en) Greg N. Frederickson, Piano-hinged Dissections: Time to Fold!, Wellesley, A K Peters, Ltd. (en), 2006 (ISBN 978-1-56881-299-1) (OCLC 65978672) (LCCN 2006012022) [lire en ligne]
Voir aussi
Articles connexes
- Démonstrations géométriques du théorème de Pythagore
- Puzzle de dissection (en)
- Tangram
Lien externe
(en) Site web de Greg N. Frederickson, professeur à l'université Purdue
Catégories :- Construction géométrique
- Histoire de la géométrie
Wikimedia Foundation. 2010.
