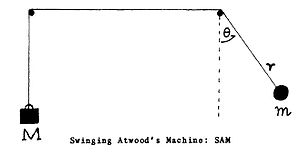
Pendule d'Atwood

Pendule d'Atwood
Le Pendule d'Atwood
Mouvement du pendule d'Atwood pour M / m = 4,5

Le Pendule d'Atwood est un mécanisme qui ressemble un peu à une simple Machine d'Atwood, si ce n'est que l'une des masses peut osciller dans un plan.

Le pendule d'Atwood possède deux degrés de liberté, la longueur du pendule r et l'angle θ. Son mouvement peut être décrit dans un espace des phases à quatre dimensions r, θ et leurs dérivées premières. La conservation de l'énergie limite le mouvement à un sous-espace à trois dimensions et il est possible d' imposer des restrictions supplémentaires au système.

Le hamiltonien de ce système s'écrit

H(r,\theta) = T + V = \frac{1}{2} M {\dot r}^2 + \frac{1}{2} m ({\dot r}^2 + r^2 \dot \theta^2) + g r (M - m \cos (\theta)),

où g est l'accélération de la pesanteur, T et V étant respectivement l' énergie cinétique et l'énergie potentielle.

Les systèmes hamiltoniens peuvent être classés en systèmes intégrables et non-intégrables. Le pendule d'Atwood est intégrable dans le cas où le rapport de masse, M/m vaut 3. Pour de nombreuses autres valeurs de ce rapport de masse, le pendule d'Atwood adopte un mouvement chaotique.

Notes et références

  • (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Swinging Atwood's machine » (voir la liste des auteurs)
  • Almeida, M.A., Moreira, I.C. and Santos, F.C. (1998) "On the Ziglin-Yoshida analysis for some classes of homogeneous hamiltonian systems", Brazilian Journal of Physics Vol.28 n.4 São Paulo Dec.
  • Barrera, Jan Emmanuel (2003) Dynamics of a Double-Swinging Atwood's machine, B.S. Thesis, National Institute of Physics, University of the Philippines.
  • Babelon, O, M. Talon, MC Peyranere (2010), "Kowalevski's analysis of a swinging Atwood's machine," Journal of Physics A-Mathematical and Theoretical Vol. 43 (8).
  • Bruhn, B. (1987) "Chaos and order in weakly coupled systems of nonlinear oscillators," Physica Scripta Vol.35(1).
  • Casasayas, J., N. B. Tufillaro, and A. Nunes (1989) "Infinity manifold of a swinging Atwood's machine," European Journal of Physics Vol.10(10), p173.
  • Casasayas, J, A. Nunes, and N. B. Tufillaro (1990) "Swinging Atwood's machine: integrability and dynamics," Journal de Physique Vol.51, p1693.
  • Chowdhury, A. Roy and M. Debnath (1988) "Swinging Atwood Machine. Far- and near-resonance region", International Journal of Theoretical Physics, Vol. 27(11), p1405-1410.
  • Griffiths D. J. and T. A. Abbott (1992) "Comment on ""A surprising mechanics demonstration,"" American Journal of Physics Vol.60(10), p951-953.
  • Moreira, I.C. and M.A. Almeida (1991) "Noether symmetries and the Swinging Atwood Machine", Journal of Physics II France 1, p711-715.
  • Nunes, A., J. Casasayas, and N. B. Tufillaro (1995) "Periodic orbits of the integrable swinging Atwood's machine," American Journal of Physics Vol.63(2), p121-126.
  • Ouazzani-T.H., A. and Ouzzani-Jamil, M., (1995) "Bifurcations of Liouville tori of an integrable case of swinging Atwood's machine," Il Nuovo Cimento B Vol. 110 (9).
  • Olivier, Pujol, JP Perez, JP Ramis, C. Simo, S. Simon, JA Weil (2010), "Swinging Atwood's Machine: Experimental and numerical results, and a theoretical study," Physica D 239, pp. 1067-1081.
  • Sears, R. (1995) "Comment on "A surprising mechanics demonstration," American Journal of Physics, Vol. 63(9), p854-855.
  • Tufillaro, N.B. (1982) Smiles and Teardrops, Senior Thesis, Reed College Physics.
  • Tufillaro, N.B., T. A. Abbott, and D. J. Griffiths (1984) "Swinging Atwood's Machine," American Journal of Physics Vol.52(10), p895.
  • Tufillaro, N.B. (1985) "Motions of a swinging Atwood's machine," Journal de Physique Vol.46, p1495.
  • Tufillaro, N.B. (1985) "Collision orbits of a swinging Atwood's machine," Journal de Physique Vol. 46, p2053.
  • Tufillaro, N.B. (1986) "Integrable motion of a swinging Atwood's machine," American Journal of Physics Vol.54(2), p142.
  • Tufillaro, N.B., A. Nunes, and J. Casasayas (1988) "Unbounded orbits of a swinging Atwood's machine," American Journal of Physics Vol.56(12), p1117.
  • Tufillaro, N.B. (1994) "Teardrop and heart orbits of a swinging Atwoods machine," The American Journal of Physics Vol.62 (3), p231-233.
  • Yehia, H.M., (2006) "On the integrability of the motion of a heavy particle on a tilted cone and the swinging Atwood machine", Mechanics Research Communications Vol. 33 (5), p711–716.

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Pendule d'Atwood de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Pendule — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. De manière générale un ou une pendule est un dispositif utilisant le principe du pendule, c est à dire constitué d un corps pouvant osciller autour d un… …   Wikipédia en Français

  • Machine d'Atwood — schéma de la machine d Atwood Atwood (1746 1807) est surtout célèbre chez les élèves de terminales math. élém. des années 1945 1972, par sa « machine » hautement didactique qui permettait de s entraîner sur la bonne application de la… …   Wikipédia en Français

  • George Atwood — né en 1746 à Londres et décédé dans cette même ville le 11 juillet 1807, est un physicien anglais. Il fit ses études à Westminster School et à Trinity College (Cambridge). Professeur de physique à Cambridge, il vérifia la valeur de l… …   Wikipédia en Français

  • Liste Des Instruments Scientifiques — Liste des instruments et équipements scientifiques Cette page dresse une liste des instruments et équipements scientifiques classés par ordre alphabétique. Note : en toute rigueur, un capteur (ou détecteur) et un transducteur (voir liste non …   Wikipédia en Français

  • Liste des instruments et équipements scientifiques — Cette page dresse une liste des instruments et équipements scientifiques classés par ordre alphabétique. Note : en toute rigueur, un capteur (ou détecteur) et un transducteur (voir liste non exhaustive en annexe) ne sont pas des instruments… …   Wikipédia en Français

  • Liste des instruments scientifiques — Liste des instruments et équipements scientifiques Cette page dresse une liste des instruments et équipements scientifiques classés par ordre alphabétique. Note : en toute rigueur, un capteur (ou détecteur) et un transducteur (voir liste non …   Wikipédia en Français

  • Liste des technologies scientifiques — Liste des instruments et équipements scientifiques Cette page dresse une liste des instruments et équipements scientifiques classés par ordre alphabétique. Note : en toute rigueur, un capteur (ou détecteur) et un transducteur (voir liste non …   Wikipédia en Français

  • Liste der Erfinder — Dies ist eine Liste von Erfindern, die die Welt mit ihren Erfindungen bereichert haben. Ein Erfinder ist jemand, der ein Problem erkannt hat, es gelöst und mindestens einmal damit Erfolg gehabt hat. Er muss nicht der erste gewesen sein; eine… …   Deutsch Wikipedia

  • Chute Libre (Physique) — Pour les articles homonymes, voir Chute libre. Une chute libre est un mouvement accéléré sous le seul effet de la pesanteur. On distingue la simple chute dans un champ de pesanteur uniforme au voisinage de la Terre (Galilée, 1605), et la chute… …   Wikipédia en Français

  • Chute libre (physique) — Pour les articles homonymes, voir Chute libre. Une chute libre est un mouvement sous le seul effet de la pesanteur. On distingue la simple chute dans un champ de pesanteur uniforme au voisinage de la Terre (Galilée, 1605), et la chute céleste… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”