Notation de Neveu
- Notation de Neveu
-
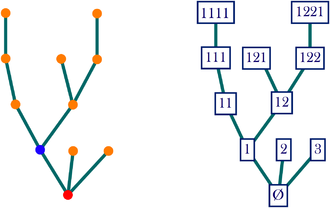
Notation de Neveu pour les sommets d'un arbre planaire.
Un arbre planaire enraciné peut être décrit de manière non ambigüe par la liste de ses sommets, chacun désigné par une suite finie d'entiers, qui sont les positions, au sein de leur fratrie, des ancêtres du sommet : c'est la notation de Neveu[1].
On utilise ici l'arbre généalogique comme métaphore pour l'arbre planaire : le sommet 2|4|3 désigne le 3ème fils du 4ème fils du 2ème fils de l'ancêtre (l'ancêtre étant lui-même désigné par la suite vide, notée 
). Par convention, l'ancêtre est le sommet initial de l'arête racine, et le sommet final de l'arête racine est le fils ainé de l'ancêtre : en tant que tel, il est noté 1. La longueur de la suite associée à un sommet est la hauteur (ou la profondeur) du sommet, i.e. la distance entre ce sommet et le début de la racine, qui représente l'ancêtre : en filant la métaphore, un sommet de hauteur n représente un individu appartenant à la n-ème génération de la population fondée par l'ancêtre.
Exemple
Exemple :
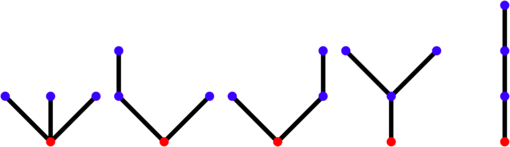
Les 5 arbres à 3 arêtes sont ainsi décrits par les 5 ensembles de mots
Remarques
Le parcours des sommets dans l'ordre lexicographique est alors le parcours en profondeur préfixé (ou parcours préfixe) d'un arbre vu comme structure de données en informatique. Autre application : avec cette notation, un arbre planaire encode commodément une réalisation de processus de Galton-Watson avec extinction. Rien ne s'oppose à définir un arbre planaire infini à l'aide de la notation de Neveu, ce qui permet d'encoder les réalisations de processus de Galton-Watson où la population ne s'éteint pas.
Notes
Voir aussi
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Notation de Neveu de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Gross-Neveu model — The Gross Neveu model is a quantum field theory model of Dirac fermions interacting via four fermion interactions.We have N Dirac fermions, psi;1, ..., psi;N. The Lagrangian density is:mathcal{L}=overline{psi} a left(ipartial!!!/ m ight) psi^a +… … Wikipedia
Processus de Galton-Watson — Le processus de Galton Watson est un processus stochastique permettant de décrire des dynamiques de populations. Sommaire 1 Historique 2 Formulation générale 3 Paramètre critique et classification des processus de Galton Watson … Wikipédia en Français
Arbre (graphe) — Pour les articles homonymes, voir Arbre (homonymie). Un arbre avec 4 feuilles et 3 nœuds internes. En théorie des graphes, un arbre est un graphe non orienté … Wikipédia en Français
Arbre de Galton-Watson — Pour les articles homonymes, voir Arbre (homonymie). Simulation d un arbre de Galton Watson avec une loi de Poisson de paramètre 1 pour loi de rep … Wikipédia en Français
Arbre (mathématiques) — Pour les articles homonymes, voir Arbre (homonymie). Pour tout ce qui concerne les arbres en théorie des graphes voir ici. Un arbre est la donnée d un ensemble E et d une relation symétrique R sur E telle que deux points distincts quelconques x… … Wikipédia en Français
Da Vinci Code — Pour l adaptation cinématographique, voir Da Vinci Code (film). Da Vinci Code Détail de la Joconde : ses yeux figurent sur la couverture du roman … Wikipédia en Français
DaVinci Code — Da Vinci Code Pour l adaptation cinématographique, voir Da Vinci Code (film). Da Vinci Code Détail de la Joconde : ses yeux figurent sur la couverture du roman Auteur Dan Brown Genre … Wikipédia en Français
Da Vinci code — Pour l adaptation cinématographique, voir Da Vinci Code (film). Da Vinci Code Détail de la Joconde : ses yeux figurent sur la couverture du roman Auteur Dan Brown Genre … Wikipédia en Français
Da vinci code — Pour l adaptation cinématographique, voir Da Vinci Code (film). Da Vinci Code Détail de la Joconde : ses yeux figurent sur la couverture du roman Auteur Dan Brown Genre … Wikipédia en Français
Gerbert d'Aurillac — Sylvestre II Pour les articles homonymes, voir Sylvestre. Sylvestre II Pape de l’Église c … Wikipédia en Français
Les 5 arbres à 3 arêtes.
