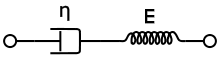
Modèle de Maxwell

Modèle de Maxwell

Le modèle de Maxwell décrit un matériau viscoélastique, c'est-à-dire ayant à la fois des propriétés élastiques et visqueuses. Ce modèle fut proposé par James Clerk Maxwell en 1867.

Définition

Représentation schématique du modèle de Maxwell.

Le modèle de Maxwell peut être représenté par un amortisseur purement visqueux et un ressort hookéen mis en série comme l'indique le schéma ci-contre. Dans cette configuration, lorsqu'une contrainte axiale est appliquée, la contrainte totale σTotal et la déformation totale γTotal peuvent être définie de la manière suivante :

σTotal = σA = σR
γTotal = γA + γR

où l'indice A désigne l'amortisseur et l'indice R le ressort.

Les contraintes de l'amortisseur et du ressort sont données respectivement par :

\sigma_{A}= \eta \dot\gamma
σR = Eγ

où E est le module élastique associé au ressort et η le coefficient de viscosité associé à l'amortisseur représentant un fluide newtonien.


Dérivons la déformation totale par rapport au temps :

\frac {d\gamma_{Total}} {dt} = \frac {d\gamma_{A}} {dt} + \frac {d\gamma_{R}} {dt} = \frac {\sigma} {\eta} + \frac {1} {E} \frac {d\sigma} {dt}

En notant la dérivée temporelle par un point, l'équation précédente se réécrit :

\frac {\dot {\sigma}} {E} + \frac {\sigma} {\eta}= \dot {\gamma}.

En multipliant cette équation par η,

\tau \dot{\sigma} + \sigma= \eta \dot {\gamma}

on a fait apparaître le temps de relaxation de Maxwell :

\tau = \frac{\eta}{E} .

La solution générale de l'équation de Maxwell s'écrit :

\sigma(t) = \frac{\eta}{\tau} \int_{-\infty}^{t} exp(-(t-t')/\tau) \dot\gamma(t') dt' .

Le module de relaxation de la contrainte dans le cadre de ce modèle s'écrit :

G * = G' + iG''

avec

G' = \frac{E\omega^2\tau^2}{1+\omega^2 \tau^2}

G'' = \frac{E\omega\tau}{1+\omega^2 \tau^2}

On peut remarquer que

\left(G'-\frac{E}{2}\right)^2 + G''^2 = \frac{E^2}{4}

est l'équation d'un cercle. Ainsi, la représentation de G'' en fonction de G', dite représentation de Cole-Cole, est un demi cercle.

Remarque :

La mise en parallèle de ces deux éléments (amortisseur et ressort) donne le modèle de Kelvin-Voigt.

Modèle de Maxwell généralisé

Le modèle de Maxwell généralisé consiste à mettre en parallèle un nombre N fini d'éléments de Maxwell. Chacun de ces éléments répond aux relations énoncées ci-dessus. La contrainte totale est la somme des contraintes de chaque élément :

\sigma(t) = \sum_{i=0}^{N}\sigma_i(t) = \sum_{i=0}^{N} \frac{\eta_i}{\tau_i} \int_{-\infty}^{t} exp(-(t-t')/\tau_i) \dot\gamma(t') dt' .

Dans ce cas, la fluide ne comporte pas qu'un seul temps de relaxation, mais une collection {τi}.

Cette équation peut se réécrire de la manière suivante :

\sigma(t) = \int_{-\infty}^{t} G(t-t') \dot\gamma(t') dt'

où on a défini le module de relaxation des contraintes de cisaillement :

G(t) = \sum_{i=0}^{N} \frac{\eta_i}{\tau_i} exp(-t/\tau_i).

Articles connexes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Modèle de Maxwell de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Modèle de Maxwell convecté supérieur — Le modèle de Maxwell convecté supérieur est une généralisation du modèle de Maxwell tenant compte des non linéarités cinématiques (mais ne tenant pas compte des non linéarités mécaniques). Ce modèle a été proposé pour la première fois par James G …   Wikipédia en Français

  • Modele atomique de Thomson — Modèle atomique de Thomson Représentation schématique du modèle de plum pudding de l atome. Dans le modèle mathématique de Thomson, les « corpuscules » (les électrons modernes) sont placés de manière non aléatoire, dans des anneaux… …   Wikipédia en Français

  • Modèle de Thomson — Modèle atomique de Thomson Représentation schématique du modèle de plum pudding de l atome. Dans le modèle mathématique de Thomson, les « corpuscules » (les électrons modernes) sont placés de manière non aléatoire, dans des anneaux… …   Wikipédia en Français

  • Modèle de plum pudding — Modèle atomique de Thomson Représentation schématique du modèle de plum pudding de l atome. Dans le modèle mathématique de Thomson, les « corpuscules » (les électrons modernes) sont placés de manière non aléatoire, dans des anneaux… …   Wikipédia en Français

  • Modèle de Kelvin-Voigt — Pour les articles homonymes, voir Voigt. Le modèle de Kelvin Voigt est un modèle de matériau viscoélastique, c est à dire présentant à la fois des propriétés élastiques et visqueuses. Définition Représentation schématique du m …   Wikipédia en Français

  • Modèle atomique de Thomson — Représentation schématique du modèle de plum pudding de l atome. Dans le modèle mathématique de Thomson, les « corpuscules » (les électrons modernes) sont placés de manière non aléatoire, dans des anneaux tournants. Le modèle atomique… …   Wikipédia en Français

  • MAXWELL (J. C.) — L’œuvre du savant britannique Maxwell a été capitale pour la théorie physique. Elle a permis d’obtenir une connaissance unifiée des phénomènes lumineux et électromagnétiques, ce qui est d’autant plus remarquable que cette unification se situe… …   Encyclopédie Universelle

  • MODÈLE — Le langage de la philosophie aiderait peu à éclairer l’origine de la notion de modèle, qui a reçu un emploi très large dans la méthodologie des sciences. Cette origine est technologique: le modèle est d’abord la «maquette», l’objet réduit et… …   Encyclopédie Universelle

  • Maxwell Type L — Constructeur Maxwell Années de production 1894 Moteur et transmission …   Wikipédia en Français

  • Maxwell Montes — Topographie d Ishtar Terra, avec Maxwell Montes au centre ouest, Lakshmi Planum à l ouest, et Fortuna Tessera à l est. Géographie et géologie Co …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”