- Équation de Mayo-Lewis
-
L'équation de Mayo-Lewis concerne l'obtention de copolymères diblocs par polyaddition. Elle permet de relier la composition instantanée du copolymère (pourcentage d'unités A et B) à la composition du mélange de monomères (pourcentage de monomères A et B). Elle donne également une idée de la structure du copolymère: statistique, à bloc, alterné…
L'équation est la suivante:
![\frac {\mathrm{d}[A]} {\mathrm{d}[B]} = \frac {[A]}{[B]} \frac {r_A[A] + [B]} {r_B[B] + [A]}](f/20f4e2d8f044bfe0ec0c20f999c0d65a.png)
Les concentrations en monomères sont données entre crochets, rA et rB sont les rapports de réactivité.
Sommaire
Contexte et démonstration
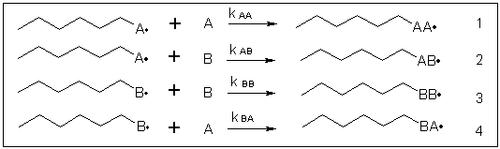
On synthétise un copolymère à partir des monomères A et B, en chaîne. À chaque addition d'un nouveau motif, on a quatre cas possibles:
Possibilités lors d'une copolymérisation en chaîne
On cherche à savoir quelle sera la proportion des unités monomères issues de A et B dans le copolymère formé. On peut écrire la vitesse de disparition des deux monomères:
![- \frac { \mathrm{d}[A] } { \mathrm{d}t } = k_{AA} [A^\bullet][A] + k_{BA} [B^\bullet][A]](b/9cb965353f44d882a46f498eece4f692.png)
![- \frac { \mathrm{d}[B] } { \mathrm{d}t } = k_{BB} [B^\bullet][B] + k_{AB} [A^\bullet][B]](7/1971084cade4ba236f5639c2793bed11.png)
Dans l'hypothèse de l'AEQS,
![k_{AB} [A^\bullet][B] = k_{BA} [B^\bullet][A]](5/78523cd09d61bf21f92a61c06eb5c2c0.png)
La concentration en centres actifs reste constante.
En faisant le rapport des deux vitesses de disparition en tenant en compte de cette cette égalité, on obtient:![\frac {\mathrm{d}[A]} {\mathrm{d}[B]} = \frac {[A]}{[B]} \frac {\frac {k_{AA}}{{k_{AB}}}[A] + [B]} {\frac {k_{BB}}{{k_{BA}}}[B] + [A]}](6/6162df80ecf2d6984059e14fb287e072.png)
On peut introduire les rapports de réactivité:
et 
.
On aboutit à:
C'est l'équation de Mayo-Lewis[1].Calcul de composition
On définit les fractions molaires:
- des unités monomères dans le copolymère formé:
![F_A = 1 - F_B = \frac {\mathrm{d}[A]} {\mathrm{d}[A] + \mathrm{d}[B]}](f/36f93e65d2426e16632dc4d0cd36ba46.png)
- des monomères dans le mélange de monomère:
![f_A = 1 - f_B = \frac {[A]} {[A] + [B]}](3/dd31e2a145cec1a5899fd17825c5ea5a.png)
alors l'équation de Mayo-Lewis devient:
À partir de cette relation, si on connait les rapports de réactivité, on peut calculer la composition d'un mélange de monomères à maintenir constante pour aboutir a un copolymère de composition donnée.
Répartition des motifs
Selon les valeurs des rapports de réactivité rA et rB, on peut avoir une idée de la structure du copolymère. Ainsi, si
alors: kAA > kAB. dans ce cas, l'unité monomère A réagira préférentiellement sur elle-même plutôt que sur une unité B. Un certain nombre de cas limites existent.- rA et rB << 1: les unités réagissent préférentiellement sur l'autre type et on obtient un copolymère alterné: (A − B − A − B − A − B − A − B − A − B − A − B)n
- rA et rB
: les unités réagissent sur elles-mêmes ou sur l'autre sorte indifféremment. Le copolymère est statistique[2]: (A − B − B − A − B − B − B − A − A − B − A − A)n - rA > 1 et rB < 1: les unités de A réagissent entre elles et celles de b sur A aussi. Le copolymère enchaîne surtout des unités A avec quelques accidents de B, jusqu'à ce que beaucoup d'unités A soient consommées: (A − A − B − A − A − A − A − B − A − A − A − A − B).
- rA > 1 et rB > 1: dans ce cas hypothétique la copolymérisation ne se ferait pas ou mal.
Calcul des rapports de réactivité
Si on pose:
![x = \frac {[A]}{[B]}](0/7b054a2a036d97848253fdd57eb62026.png)
et 
, l'équation de Mayo-Lewis devient: 
On peut préparer des copolymères de compositions différentes et tracer
en fonction de 
. La courbe obtenue est une droite dont la pente et l'ordonnée à l'origine permettent de remonter aux rapports de réactivité. D'autres méthodes existent.Références
Voir aussi
- des unités monomères dans le copolymère formé:
Wikimedia Foundation. 2010.
