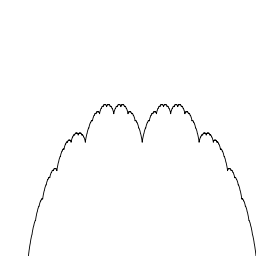
Courbe du blancmanger

Courbe du blancmanger
Blancmange-function.svg

En mathématiques, la courbe du blancmanger est une courbe fractale. Elle est aussi connue comme la courbe de Takagi, d'après Teiji Takagi qui l'a décrite en 1903, ou comme la courbe Takagi–Landsberg, une généralisation de la courbe. Le nom blancmanger vient de sa ressemblance au pudding du même nom. C'est un cas particulier de courbe de De Rham (en). .

La fonction blancmanger est définie sur [0; 1] par :

{\rm blanc}(x) = \sum_{n=0}^\infty {s(2^{n}x)\over 2^n},

où s(x) est définie par s(x)=\min_{n\in{\bold Z}}|x-n|, c'est-à-dire que s(x) est la distance entre x et l'entier le plus proche. La somme infinie blanc(x) converge pour tout x, mais la courbe résultante est une fractale. La fonction blancmanger est continue (en fait, uniformément continue) mais non dérivable.

La courbe Takagi–Landsberg en est une généralisation donnée par la relation :

T_w(x) = \sum_{n=0}^\infty w^n s(2^{n}x)

pour un paramètre w; donc la courbe du blancmanger est le cas w = 1 / 2. La valeur H = − log 2w est connue comme le paramètre de Hurst. La fonction peut-être étendue à tous les réels : appliquer la définition ci-dessus montre que la fonction se répète sur chaque intervalle unitaire.

Sommaire

Construction graphique

La courbe du blancmanger peut être construite à partir des fonctions en dents de scie si la somme infinie est approximée par les premiers termes. Sur les illustrations ci-dessous, les fonctions en dents de scie (en rouge) sont progressivement ajoutées à la courbe à chaque étape.

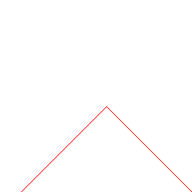
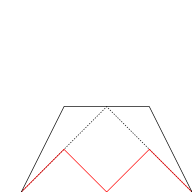
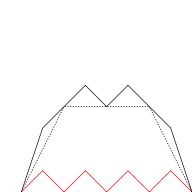
Blancmange-approx1.svg Blancmange-approx2.svg Blancmange-approx3.svg Blancmange-approx4.svg
n = 0 n ≤ 1 n ≤ 2 n ≤ 3

Intégration de la courbe

Étant donné que l'intégrale de la fonction blanc sur l'intervalle [0; 1] vaut 1/2, la relation blanc(x) = blanc(2x) / 2 + s(x) permet de calculer l'intégrale. Le calcul est récursif avec un temps de calcul de l'ordre du logarithme de la précision requise.

\begin{align} I(x) &= \int_0^x{\rm blanc}(x)\,\mathrm{d}x,\\ I(x) &=\begin{cases} 1/2+I(x-1) & \text{si }x \geq 1\\ 1/2-I(1-x) & \text{si }1/2 < x < 1 \\ I(2x)/4+x^2/2 & \text{si } 0 \leq x \leq 1/2 \\ -I(-x) & \text{si } x < 0 \end{cases} \\ \int_a^b{\rm blanc}(x)\,\mathrm{d}x &= I(b) - I(a). \end{align}

Dimension fractale

La courbe de Takagi-Landsberg (\textstyle{f(x) = \sum_{n=0}^\infty {w^n s(2^{n}x)}}) a pour dimension de Hausdorff[1] :

D_H = 2+\dfrac{\log(w)}{\log(2)}.

La dimension de Hausdorff de la courbe du blancmanger, pour laquelle w = 1 / 2, vaut donc 1, malgré son aspect fractal.

Références

  1. ↑ (en) Benoit Mandelbrot, Gaussian self-affinity and Fractals (Hunt cité par Mandelbrot) (ISBN 0-387-98993-5) 

(en) Cet article est partiellement ou en totalité issu de l’article en anglais intitulé « Blancmange curve » (voir la liste des auteurs)

Lien externe

Takagi Explorer


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Courbe du blancmanger de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”