- Arc capable
-
Le lieu des points M tels que
donné est l'arc de cercle capable 
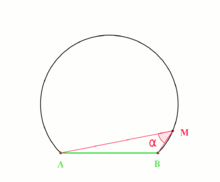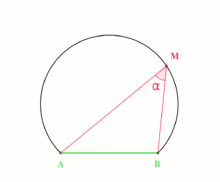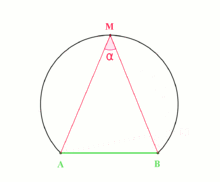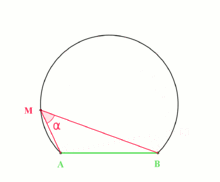
.En géométrie euclidienne plane, la notion d'arc capable répond à la question suivante : Etant donnés deux points A et B, quel est l'ensemble des points M du plan tel que l'angle
soit égal à une valeur constante donnée α ?En fait sauf dans le cas où A, B, et M sont alignés (et dans ce cas le lieu cherché est la droite (AB) ), le lieu des points M est situé sur un arc de cercle dont [AB] est une corde. On l'appelle l'arc capable. On dit que le segment [AB] est vu depuis l'arc sous l'angle α ou encore que l'arc
est capable d'inscrire un angle de la mesure α.Le théorème de l'arc capable est très lié au théorème de l'angle inscrit dont on peut considérer qu'il est la réciproque.
La construction des arcs capables était une technique utilisée autrefois pour déterminer la position des navires.
Sommaire
Théorème de l'arc capable
Théorème — Soient A et B deux points du plan et α un réel donné. L'ensemble des points M du plan différents de A et B tels que
est :- la droite (AB) privée des points A et B si
- un cercle passant par A et B et privé des points A et B sinon.
Dans la formulation du théorème ci-dessus
désigne un angle angle orienté. On peut aussi reformuler ce résultat en considérant l'angle géométrique :Théorème — Soient A et B deux points du plan et α un réel donné tel que 0 < α < π. L'ensemble des points M du plan différents de A et B tels que
est un arc de cercle ouvert ( c'est-à-dire dont les extrémités A et B sont exclues).Cet arc est appelé l'arc capable
.Pour la démonstration, on se reportera au Théorème de l'angle inscrit.
Construction géométrique d'un arc capable
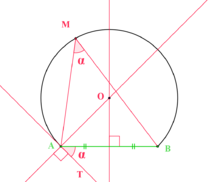Le Centre O du cercle porteur de l'arc capable est situé à l'intersection de la médiatrice de la corde [AB] et de la perpendiculaire en A à la tangente [AT).Pour construire un arc capable, il est bon d'avoir remarqué que lorsque M tend vers A, [MB] tend vers la corde [AB] et (MA) tend vers la tangente au cercle en A, que nous noterons [AT). L'angle entre la tangente [AT) au cercle en A et la corde [AB] a donc pour mesure α. L'article sur le théorème de l'angle inscrit propose une démonstration de cette propriété.
En utilisant un rapporteur et en reportant l'angle α en A, on peut donc construire la tangente au cercle en A. Le Centre O du cercle porteur de l'arc capable est situé à l'intersection de la médiatrice de la corde [AB] et de la perpendiculaire en A à la tangente [AT).
Application
Cette technique est l'une des méthodes utilisées autrefois par les marins, dans le cadre de la navigation côtière, pour déterminer la position du navire. Normalement conçut pour déterminer la latitude en mesurant la hauteur du soleil à midi au-dessus de l'horizon, le sextant, lorsqu'il est utilisé dans le plan horizontal, permet de mesurer l'angle entre deux objets. Ainsi, en prenant à l'horizon deux amers, c'est-à-dire deux points de repères identifiés, comme par exemple un phare, on peut mesurer l'angle entre ces deux points, et ensuite tracer, sur la carte, l'arc capable correspondant à ces deux points et à l'angle mesuré. En répétant l'opération avec deux autres points, on obtient la position du navire sur la carte à l'intersection des deux arcs capables.
Voir aussi
Catégories :- Théorème de géométrie
- Cercle et sphère
- Angle
- la droite (AB) privée des points A et B si
Wikimedia Foundation. 2010.
