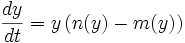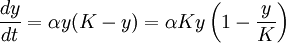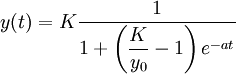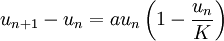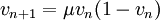Équation logistique

Modèle de Verhulst

En dynamique des populations, le modèle de Verhulst est un modèle de croissance proposé par Pierre François Verhulst vers 1840 ^[1]. Verhulst a proposé ce modèle en réponse au modèle de Malthus qui proposait un taux d'accroissement constant sans frein conduisant à une croissance exponentielle de la population.

Le modèle de Verhulst imagine que le taux de natalité et le taux de mortalité sont des fonctions affines respectivement décroissante et croissante de la taille de la population. Autrement dit, plus la taille de la population augmente, plus son taux de natalité diminue et son taux de mortalité augmente. Verhulst pose d'autre part que, lorsque les populations sont de petites tailles, elles ont tendance à croître.

Le même modèle est utilisable pour des réactions autocatalytiques, dans lesquelles l'augmentation des individus touchés est proportionnelle à la fois au nombre d'individus déjà touchés et au nombre d'individus qui peut encore être touchés.

Ce modèle conduit, en temps continu, à une fonction logistique et en temps discret à une suite logistique dont la particularité est d'être, dans certaines circonstances, chaotique

Mise en place mathématique

Si on appelle

y la taille de la population
m(y) le taux de mortalité
n(y) le taux de natalité

la taille de la population suit l'équation différentielle

$\frac{dy}{dt}= y\left(n(y) - m(y)\right)$

Si m et n sont des fonction affines respectivement croissante et décroissante alors n - m est une fonction affine décroissante. Si d'autre part, pour y tendant vers 0, la croissance est positive, l'équation peut s'écrire

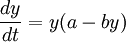$\frac{dy}{dt}= y(a-by)\,$ avec a et b deux réels positifs

Puis, en posant K=a/b, l'équation devient

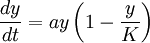$\frac{dy}{dt}= ay\left(1-\frac yK\right)$ avec a > 0 et K > 0

Une observation immédiate montre que

la fonction constante K est solution de cette équation
si y < K alors la population croît
si y > K alors la population décroît.

Le paramètre K est appelé la capacité d'accueil.

Le modèle auto-catalytique conduit à la même équation (accroissement proportionnel à la population touchée et à la population restante)

$\frac{dy}{dt}= \alpha y (K- y) = \alpha Ky\left(1-\frac yK\right)$

Résolution en temps continu

Article détaillé : fonction logistique (Verhulst).

La recherche des fonctions strictement positives définies sur 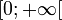$[0; + \infty[$ et vérifiant le système

$y (0) = y 0$
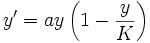
$y' = ay\left(1-\frac yK\right)$

Conduit à la solution logistique

$y(t) = K\dfrac{1}{1+\left(\dfrac K{y_0}-1\right)e^{-at}}$

Où l'on observe que la population tend vers la capacité d'accueil K, qu'elle est croissante si la population initiale est inférieure à la population d'accueil et décroissante sinon.

Résolution en temps discret

Article détaillé : suite logistique.

En temps discret, le modèle se transforme en

$u_{n+1} - u_n = au_n\left(1-\frac{u_n}{K}\right)$

Puis, en posant

$a + 1 = μ$
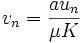
$v_n = \frac{au_n}{\mu K}$

la relation de récurrence devient

$v_{n+1}=\mu v_n (1 - v_n)\,$

C'est sous cette forme qu'elle est étudiée comme suite logistique. Cette suite, bien que très simple par son expression, peut conduire à des résultats très variés ; son comportement varie suivant les valeurs de $μ$ :

pour μ compris entre 1 et 3, c'est-à-dire a compris entre 0 et 2, la suite $(v n)$ converge vers 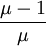$\frac {\mu - 1}{\mu}$ et l'on retrouve bien une suite $(u n)$ convergeant vers K
pour μ supérieur à 3, la suite $(v n)$ peut , selon les valeurs de μ, osciller entre 2, 4, 8, 16.... valeurs ou bien être chaotique.

Voir aussi

Liens internes

Sources

Pierre-François Verhulst, « Notice sur la loi que la population poursuit dans son accroissement », dans Correspondance mathématique et physique, n^o 10, 1838, p. 113-121 [[pdf] texte intégral (page consultée le 31/05/2009)]
Pierre-François Verhulst, « Recherches mathématiques sur la loi d'accroissement de la population », dans Nouveaux Mémoires de l'Académie Royale des Sciences et Belles-Lettres de Bruxelles, n^o 18, 1845, p. 1-42 [[pdf] texte intégral (page consultée le 30/05/2009)]
Pierre-François Verhulst, « Deuxième mémoire sur la loi d'accroissement de la population », dans Mémoires de l'Académie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique, n^o 20, 1847, p. 1-32 [[pdf] texte intégral (page consultée le 31/05/2009)]

Liens externes

Mathématiques en dynamiques des populations de Christellle Magal
Bernard Delmas, Pierre-François Verhulst et la loi logistique de la population, dans Mathématics and Social Sciences (n° 167, 2004)

Notes et références

↑ On trouve selon les sources 1838 [1], 1844[2] ou 1846 [3]

Ce document provient de « Mod%C3%A8le de Verhulst ».

Catégories : Écologie des populations | Équation différentielle | Démographie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation logistique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Equation — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation (mathématiques) — Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation symétrique — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation vectorielle — Équation (mathématiques) Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation — Cet article concerne les équations mathématiques dans leur généralité. Pour une introduction au concept, voir Équation (mathématiques élémentaires). … Wikipédia en Français
Équation différentielle logistique — Modèle de Verhulst En dynamique des populations, le modèle de Verhulst est un modèle de croissance proposé par Pierre François Verhulst vers 1840 [1]. Verhulst a proposé ce modèle en réponse au modèle de Malthus qui proposait un taux d… … Wikipédia en Français
BIODÉMOGRAPHIE - Logistique des populations naturelles — Les populations naturelles sont des ensembles fluctuants d’individus de même espèce. Elles se développent et se déploient dans un espace écologique où elles côtoient une multitude d’autres espèces. De tels ensembles multispécifiques constituent… … Encyclopédie Universelle
Courbe logistique — Fonction logistique (Verhulst) Fonction logistique, cas particulier: sigmoïde. En mathématiques les fonctions logistiques sont les fonctions ayant pour expression où K et r sont des réels positifs et a un réel quelconque … Wikipédia en Français
Fonction Logistique (Verhulst) — Fonction logistique, cas particulier: sigmoïde. En mathématiques les fonctions logistiques sont les fonctions ayant pour expression où K et r sont des réels positifs et a un réel quelconque … Wikipédia en Français
Fonction logistique (Verhulst) — Fonction logistique, cas particulier: sigmoïde. En mathématiques, les fonctions logistiques sont les fonctions ayant pour expression où K et r sont des réels positifs et … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Équation logistique

Modèle de Verhulst

Sommaire

Mise en place mathématique

Résolution en temps continu

Résolution en temps discret

Voir aussi

Liens internes

Sources

Liens externes

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Équation logistique

Modèle de Verhulst

Sommaire

Mise en place mathématique

Résolution en temps continu

Résolution en temps discret

Voir aussi

Liens internes

Sources

Liens externes

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link