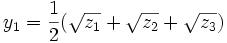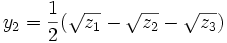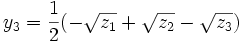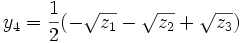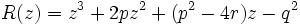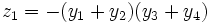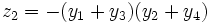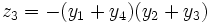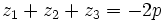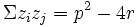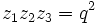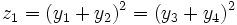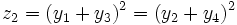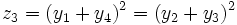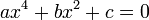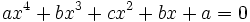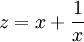Équation du quatrième degré

Équation quartique

En mathématique, une équation quartique est une équation polynomiale de degré quatre.

Les équations quartiques ont été résolues dès que furent connues les méthodes de résolutions des équations du troisième degré. Ont été développées successivement la méthode de Ferrari (1522 - 1565) et la méthode de Descartes (1596 - 1650)

La méthode décrite ci-dessous est issue des propriétés des polynômes symétriques construits à partir des n racines d'un polynôme de degré n.

Sommaire

1 Formules
2 Inventaires des cas
3 Principe de la méthode
4 Equations particulières
5 Voir aussi
- 5.1 Article connexe
- 5.2 Sources

Formules

L'équation

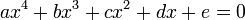$ax^4 + bx^3+ cx^2 + dx + e = 0\,$ (1)

se ramène, après division par a et changement de variable 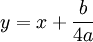$y = x + \frac{b}{4a}$ à l'équation

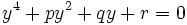$y^4 + py^2 + qy + r = 0\,$ (2)

dont les solutions sont

$y_1 = \frac 12 ( \sqrt{z_1} + \sqrt{z_2} + \sqrt{z_3})$

$y_2 =\frac 12 ( \sqrt{z_1} - \sqrt{z_2} - \sqrt{z_3})$

$y_3 = \frac 12 (-\sqrt{z_1} + \sqrt{z_2} - \sqrt{z_3})$

$y_4 = \frac 12 (- \sqrt{z_1} - \sqrt{z_2} + \sqrt{z_3})$

où $z 1$ , $z 2$ et $z 3$ sont les trois racines du polynôme R résultant de degré trois.

$R(z) = z^3 + 2pz^2 + (p^2 - 4r)z -q^2\,$

Ces trois racines se déterminant à l'aide de la méthode de Cardan.

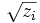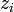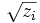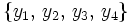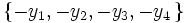Par $\sqrt{z_i}$ , il faut entendre, un des nombres dont le carré vaut $z_i\,$ . On remarque que changer $\sqrt{z_i}$ en son opposé transforme l'ensemble $\{y_1,\,y_2,\,y_3,\,y_4\}$ en $\{-y_1,-y_2, -y_3,-y_4\,\}$ . Il faut donc choisir les bonnes racines carrées. Ce sont celles telles que le produit 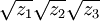$\sqrt{z_1} \sqrt{z_2} \sqrt{z_3}$ vaut - q.

Inventaires des cas

Dans le cas où les coefficients p, q et r sont réels, on remarque que le produit des racines du polynôme R est $q 2$ , on est donc limité sur la forme des racines du polynôme R et sur les solutions de l'équation quartique.

Si les trois racines de R sont réelles positives, on obtient 4 valeurs réelles.
Si les trois racines de R sont réelles et que deux sont négatives, on obtient deux couples de complexes conjugués.
si R possède une racine réelle et deux racines complexes conjuguées, la racine réelle est positive et on obtient 2 valeurs réelles et deux complexes conjugués.

Principe de la méthode

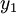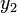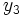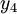Il s'agit de trouver une expression faisant intervenir les 4 racines $y_1\,$ , $y_2\,$ , $y_3\,$ et $y_4\,$ , et ne permettant d'obtenir, par permutations, que 3 valeurs distinctes.

C'est le cas par exemple de 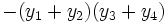$-(y_1 + y_2)(y_3 + y_4)\,$ qui, par permutations, ne permet de donner que les valeurs

$z_1 = -(y_1 + y_2)(y_3 + y_4)\,$

$z_2 = -(y_1 + y_3)(y_2 + y_4)\,$

$z_3 = -(y_1 + y_4)(y_2 + y_3)\,$

Tout polynôme symétrique en 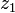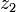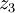$z_1\,$ , $z_2\,$ , $z_3\,$ pourra être exprimé comme polynôme symétrique de $y_1\,$ , $y_2\,$ , $y_3\,$ , $y_4\,$ .

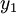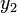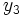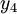En particulier, les coefficients du polynôme 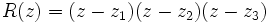$R(z) = (z - z_1)(z - z_2)(z - z_3)\,$ pourront s'exprimer à l'aide de p, q et r. Il est certain que la propriété

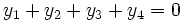$y_1 + y_2 + y_3 + y_4 = 0\,$ facilite les calculs.

On démontre en effet que

$z_1 + z_2 + z_3 = - 2p\,$

$\Sigma z_iz_j = p^2-4r\,$

$z_1z_2z_3 = q^2\,$

Les trois réels 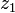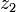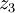$z_1\,$ , $z_2\,$ , $z_3\,$ sont alors solutions de l'équation

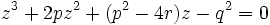$z^3 +2pz^2 + (p^2 - 4r)z -q^2 = 0\,$ (3)

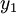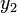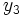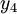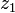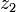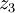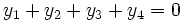Il reste maintenant à retrouver $y_1\,$ , $y_2\,$ , $y_3\,$ , $y_4\,$ en fonction de $z_1\,$ , $z_2\,$ , $z_3\,$ sachant que $y_1 + y_2 + y_3 + y_4 = 0\,$ .

On remarque alors que

$z_1 = (y_1 + y_2)^2 = (y_3 + y_4)^2\,$

$z_2 = (y_1 + y_3)^2 = (y_2 + y_4)^2\,$

$z_3 = (y_1 + y_4)^2 = (y_2 + y_3)^2\,$

donc que

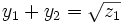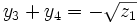
$y_1 + y_2 = \sqrt{z_1}$ et $y_3 + y_4 = - \sqrt{z_1}\,$

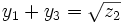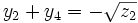
$y_1 + y_3 = \sqrt{z_2}$ et $y_2 + y_4 = - \sqrt{z_2}\,$

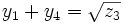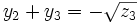
$y_1 + y_4 = \sqrt{z_3}$ et $y_2 + y_3 = - \sqrt{z_3}\,$

(il faut comprendre ici la notation 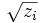$\sqrt{z_i}\,$ comme une des racines carrées de $z_i\,$ ).

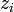Les valeurs de 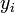$y_i\,$ se retrouvent alors par simple addition.

Equations particulières

Parmi les équations de degré quatre, certaines, particulières, peuvent se résoudre uniquement à l'aide des équations quadratiques, c'est le cas des équations bicarrées et des équation symétriques.

Équations bicarrées

Elles s'écrivent sous la forme

$ax^4 + bx^2 + c = 0\,$

et se résolvent par changement de variable

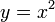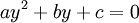
$y = x^2\,$ et $ay^2 + by + c = 0\,$

Équations quasi-symétriques

Les équations du type

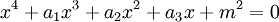$x^4+a_1x^3+a_2x^2+a_3x+m^2=0\,$ , avec 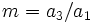$m = a_3/a_1\,$ , peuvent être résolues à l'aide de la méthode d'Ana Flores : en divisant l'équation par 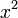$x^2\,$ , on obtient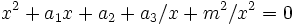

$x^2+a_1x+a_2+a_3/x+m^2/x^2=0\,$

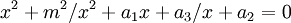
$x^2+m^2/x^2+a_1x+a_3/x+a_2=0\,$

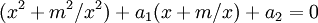
$(x^2+m^2/x^2)+a_1(x+m/x)+a_2=0\,$

À l'aide du changement de variable

$z=x + m/x\,$

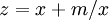
et sachant que

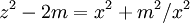
$z^2 - 2m= x^2 + m^2/x^2\,$

on obtient

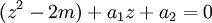$(z^2-2m)+a_1z+a_2=0\,$ .

Cette équation admet au plus deux solutions 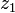$z_1\,$ et $z_2\,$ .

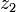Les racines de l'équation initiale peuvent être obtenues en résolvant

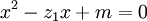
$x^2 - z_1 x+m=0\,$

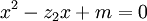$x^2 - z_2 x+m=0\,$ .

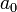Si $a_0\,$ est différent de 1 dans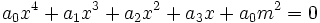

$a_0x^4+a_1x^3+a_2x^2+a_3x+a_0m^2=0\,$

la méthode s'applique toujours. Il suffit de diviser toute l'équation par $a_0\,$ .

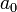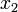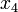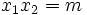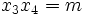L'équation quasi-symétrique a la propriété suivante : si $x 1$ , $x_2\,$ , et $x 3$ , $x_4\,$ sont les racines de l'équation, alors $x_1x_2=m\,$ et $x_3x_4=m\,$ .

Équations symétriques

Elles s'écrivent sous la forme

$ax^4 + bx^3 + cx^2 + bx + a = 0\,$

(il s'agit d'un cas particulier du cas précédent) et se résolvent par le changement de variable

$z = x + \frac {1}{x}\,$

et la résolution de

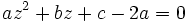$az^2 + bz + c - 2a = 0\,$ .

Voir aussi

Sources

Jacqueline Lelong-Ferrand, Jean-Marie Arnaudies, Cours mathématiques. Algèbre, Éditions Dunod.
Petite encyclopédie de mathématiques, Éditions Didier.

Portail des mathématiques

Ce document provient de « %C3%89quation quartique ».

Catégorie : Équation polynomiale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation du quatrième degré de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires: