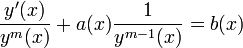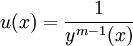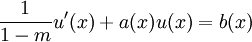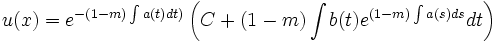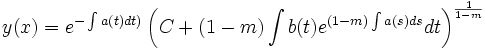Équation différentielle de bernoulli

Équation différentielle de Bernoulli

L'équation différentielle de Bernoulli est une équation différentielle du premier ordre de la forme :

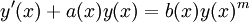$y'(x) + a(x)y(x)= b(x)y(x)^m \;$ avec m différent de 0 et 1.

Où 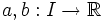$a,b:I \rightarrow \mathbb{R}$ et I est un intervalle ouvert. En général m est un entier naturel, mais on peut prendre m réel à condition de prendre y strictement positif. En général, a et b sont des fonctions continues.

Cette équation a été proposée à la résolution par Jacques Bernoulli en 1695 et résolue un an plus tard par Leibniz par changement de variable se ramenant à une équation différentielle linéaire. C'est la méthode encore employée aujourd'hui pour résoudre cette équation.

En supposant y strictement positif sur l'intervalle I, on peut diviser l'équation par $y m (x)$ et on obtient

$\frac{y'(x)}{y^m(x)} + a(x)\frac{1}{y^{m-1}(x)} = b(x)$

En posant

$u(x) = \frac{1}{y^{m-1}(x)}$

on obtient l'équation différentielle linéaire

$\frac{1}{1-m}u'(x) + a(x)u(x) = b(x)$

dont la solution générale est

$u(x) = e^{-(1-m)\int a(t)dt)}\left(C + (1-m)\int b(t)e^{(1-m)\int a(s)ds}dt\right)$

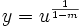
ce qui donne pour la fonction $y = u^{1\over 1-m}$

$y(x) = e^{- \int a(t)dt)}\left(C + (1-m)\int b(t)e^{(1-m)\int a(s)ds}dt\right)^{1 \over 1-m}$

Si la fonction y passe par le point 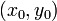$(x_0,y_0)\;$ alors la solution de cette équation est :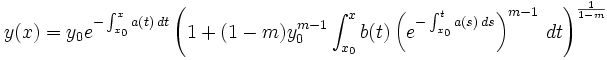

$y(x)= y_0 e^{-\int_{x_0}^{x} a(t)\, dt} \left(1+(1-m)y_0^{m-1} \int_{x_0}^{x} b(t)\left(e^{-\int_{x_0}^{t} a(s)\, ds}\right)^{m-1} \, dt\right)^{\frac{1}{1-m}}$

Des solutions peuvent être cherchées dans des fonctions non nécessairement positives, mais alors de nombreuses précautions sont à prendre quant aux domaines de validité.

Sources

une histoire des équations différentielles
Cours de mathématiques (Tome 4) de J.Lelong-Ferrand et J.M. Arnaudies

Portail des mathématiques

Ce document provient de « %C3%89quation diff%C3%A9rentielle de Bernoulli ».

Catégorie : Équation différentielle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation différentielle de bernoulli de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Equation differentielle de Bernoulli — Équation différentielle de Bernoulli L équation différentielle de Bernoulli est une équation différentielle du premier ordre de la forme : avec m différent de 0 et 1. Où et I est un intervalle ouvert. En général m est un entier naturel, mais … Wikipédia en Français
Équation différentielle de Bernoulli — Une équation différentielle de Bernoulli est une équation différentielle du premier ordre de la forme : où m est différent de 0 et 1 et où a et b sont des applications définies sur un intervalle ouvert I de ℝ et à valeurs réelles. En général … Wikipédia en Français
Équation différentielle de Riccati — Équation de Riccati En mathématiques, une équation de Riccati est une équation différentielle ordinaire de la forme . Où , et sont trois fonctions, souvent choisies continues à valeurs réelles sur un intervalle commun mais on les rencontre… … Wikipédia en Français
Equation differentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français
Equation différentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français
Équation différentielle du premier ordre — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français
Équation différentielle ordinaire — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français
Équation différentielle — En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de dérivation auquel l une des fonctions inconnues a… … Wikipédia en Français
Équation différentielle stochastique — Une équation différentielle stochastique (EDS) est une généralisation de la notion d équation différentielle prenant en compte un terme de bruit blanc. Les EDS permettent de modéliser des trajectoires aléatoires, tels des cours de bourse ou les… … Wikipédia en Français
Bernoulli — Famille Bernoulli Les Bernoulli qui se sont illustrés dans les mathématiques et la physique, sont issus de Nicolas Bernoulli (1623 1708), descendant d une famille ayant émigré d Anvers à Bâle à la fin du XVIe siècle. Les représentants les… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Équation différentielle de bernoulli