Énergie de Gibbs

Potentiels thermodynamiques
Énergie interne	U(S,V,N)
Énergie libre	F(T,V,N) = U − TS
Enthalpie	H(S,p,N) = U + pV
Enthalpie libre	G(T,p,N) = U + pV − TS
modifier

La fonction enthalpie libre G a été introduite par Willard Gibbs. Elle est associée au second principe de la thermodynamique, principe d’évolution des systèmes physico-chimiques.

Le second principe stipule que toute transformation réelle s’effectue avec création d’entropie, c’est-à-dire que le bilan entropique correspondant à la somme des variations d'entropie du système et du milieu extérieur, est positif.

.

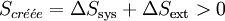La fonction entropie peut être utilisée pour l’étude de l’évolution d’un système thermodynamique. En effet pour un système isolé l’entropie passe par un maximum à l’équilibre donc toute évolution doit aller dans ce sens.

En général, intuitivement on pense qu’un équilibre est atteint lorsque l’énergie est minimale. C’est le cas de l’énergie potentielle (gravitation, électromagnétisme…). De plus dans le cas de l’entropie il faut étudier en plus du système, l’évolution de l’entropie du milieu extérieur.

Gibbs a défini une nouvelle fonction qui prend en compte ces deux remarques.

L’enthalpie libre G se comporte en effet comme une fonction potentielle et intègre le comportement du milieu extérieur. De plus elle est la fonction d'état la plus appropriée pour étudier les équilibres chimiques réalisés à la température T et à pression constante ce qui est le lot de nombreuses réactions effectuées à l'air libre, à la pression atmosphérique.

Sommaire 1 Définition 2 Différentielle de G = H-TS 2.1 Cas d'une pile réversible qui fonctionne à T et p constantes 2.2 Cas d’une réaction chimique à T et p constantes, irréversible par nature 3 Voir aussi

Définition

Considérons une réaction chimique effectuée à la température T et à pression constante p. Le travail n’est dû qu’aux forces de pression (pas de montage électrochimique donnant du travail électrique). Soit Q_P la chaleur mise en jeu par le système réactionnel. Comme la pression p est constante, la variation d'enthalpie du système est égale à la chaleur mise en jeu : ΔH_sys = Q_P.

Appliquons le second principe :

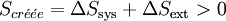
Or la chaleur fournie par le système est reçue par le milieu extérieur, donc son signe change (règle des signes) : − Q_P = − ΔH_sys.

La variation d’entropie du milieu extérieur devient : .

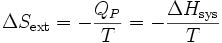Le bilan entropique s’écrit :

.

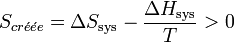Multiplions les deux membres de cette inégalité par − T, on obtient :

.

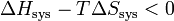On obtient la nouvelle fonction d’état

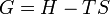
A température et pression constante

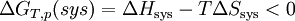
La réaction ne peut se produire que dans le sens correspondant à la diminution de la fonction G_T,p(sys) ; l’équilibre étant atteint pour le minimum de G_T,p(sys).

Différentielle de G = H-TS

dG = dH − TdS − SdT,

or H = U + pV

dH = dU + pdV + Vdp

dG = dU + pdV + Vdp − TdS − SdT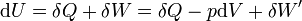

Premier principe :

Le travail correspond soit aux forces de pression − pdV soit au travail électrique dans un montage de pile δW'.

Second principe :

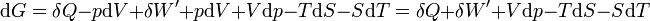
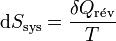
d’où

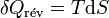
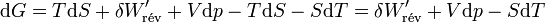
Il s'ensuit: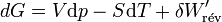

Cas d'une pile réversible qui fonctionne à T et p constantes

Une pile électrique est un dispositif particulier qui permet de transformer l'énergie chimique mise en jeu au cours d'une réaction d'oxydo-réduction, en énergie électrique fournie au milieu extérieur : W'. Si la pile débite sous une faible tension on peut considérer que la réaction se produit de façon proche de la réversibilité et qu'ainsi, à chaque instant, l'état de la pile est proche d'un état d'équilibre. Ce mode de fonctionnement peut être réalisé en introduisant dans le circuit extérieur une contre tension proche, à un près, de la force électromotrice de la pile.

Dans ces conditions, à T et p constantes :

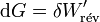et pour une transformation finie :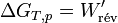

La variation d’enthalpie libre dans une pile réversible correspond au travail électrique fourni au milieu extérieur.

Si la pile n’est pas réversible comme toute pile réelle, le deuxième principe s’applique par l’inégalité de Clausius (voir entropie): 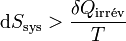. En reprenant les calculs, on aboutit à l’inégalité suivante :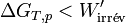

Il s'ensuit: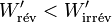 et comme le travail fourni par le système électrochimique est négatif d'après la règle des signes, il faut prendre en compte la valeur absolue de ce travail :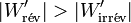

Le travail électrique fourni par la pile est plus important si la pile se rapproche d’un fonctionnement réversible, c’est-à-dire avec un déséquilibre de tension faible. L’irréversibilité se manifeste ici par effet Joule .

Cas d’une réaction chimique à T et p constantes, irréversible par nature

S’il n’y a pas de montage de pile, il n’y a pas de travail électrique, δW' = 0.

La réaction chimique est irréversible et le deuxième principe s’applique par l’inégalité de Clausius (voir entropie): .

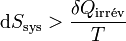Si on reprend les calculs de la différentielle dG, on obtient alors l’inégalité :

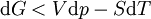
Or ici T et p sont constantes:

dG_T,p(sys) < 0 et pour une réaction chimique réelle:

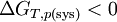
On peut exprimer la variation d'enthalpie libre en fonction de l'entropie créée:

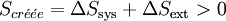
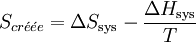, multiplions par − T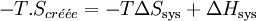

Il s'ensuit: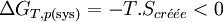

Par conséquent toute réaction chimique ne peut progresser que si l’enthalpie libre du système réactionnel diminue. Lorsque cette fonction atteint un minimum, le système est à l’équilibre.

La fonction G_T,p(sys) permet donc de définir le sens de la réaction et son positionnement à l’équilibre. C’est la fonction la plus importante pour l’étude des équilibres chimiques.

Remarque: Un changement d'état physique peut être considéré comme une réaction chimique particulière qui peut être effectuée en se rapprochant de la réversibilité. Par exemple la fusion de la glace peut être effectuée à O^°C + ε . Dans ce cas l'entropie créée est proche de zéro. Il s'ensuit que 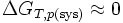. C'est pourquoi on parle alors d'équilibre de changement d'état.

Voir aussi

• Entropie
• Équilibre chimique

• Portail de la physique
• Portail de la chimie