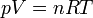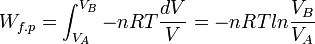Réversibilité thermodynamique

La réversibilité et l’irréversibilité sont des concepts importants en physique et tout particulièrement en thermodynamique.

Tout le monde a fait les expériences suivantes :

• un morceau de verre se brise^[1] sur le sol et il ne se reconstitue jamais de lui-même,
• en revanche, on peut tirer sur un élastique, le déformer et, dans une certaine limite, quand on le relâche cet élastique retrouve un état semblable à son état initial.

La première expérience est typique d'un comportement irréversible, la seconde est ce qui s'approche le plus d'une transformation réversible. Aussi simples qu'ils puissent paraître ces deux exemples illustrent respectivement la possibilité ou l'impossibilité pour un système de retrouver spontanément et de manière exacte son état immédiatement antérieur à une modification.

Sommaire 1 Évolution de l'univers et flèche du temps 2 Définition 3 La réversibilité en mécanique et position du problème 4 Phénomènes microscopiques et macroscopiques 5 L'irréversibilité thermodynamique 5.1 Conditions d'irréversibilité 5.2 Expression et interprétation 5.3 Remarques 6 Transformation réversible 6.1 Application au calcul du travail des forces de pression 7 Exemples 7.1 Cycle compression-détente d'un gaz 7.2 Transfert thermique 7.2.1 Étude de la variation d'entropie 7.2.2 Transformation quasi-statique 7.3 Expérience de Joule quasistatique 7.4 Interprétation microscopique 7.5 Frottement de Coulomb 8 Les phénomènes à hystérésis 9 Couplages linéaires de phénomènes irréversibles 10 L'irréversibilité en mécanique quantique 11 Irréversibilité et apparition de structure organisée 12 Irréversibilité en thermochimie 13 Notes et références 14 Voir aussi 14.1 Articles connexes 14.2 Liens externes 14.3 Bibliographie

Évolution de l'univers et flèche du temps

Définition

D'une manière générale on dit qu'un phénomène est réversible, si une modification infinitésimale des conditions permet à un système, qui a évolué sous l'influence de ce phénomène, de retrouver son état immédiatement antérieur. En thermodynamique par exemple, la notion d'évolution réversible est quantitative puisqu'on la définit comme une évolution pour laquelle aucune entropie n'est produite.

Par opposition, tous les autres phénomènes sont dits irréversibles. Ce sont ceux pour lesquels il est impossible de retrouver l'état immédiatement antérieur d'un système sans modifications importantes des conditions. Cela se traduit en thermodynamique par une production d'entropie.

Pour le physicien, tous les phénomènes sont irréversibles, et la réversibilité est un cas limite mathématique ou une idéalisation.

La réversibilité en mécanique et position du problème

La mécanique classique, telle que fondée par Newton notamment, suppose la réversibilité des phénomènes de manière implicite. En effet dans toutes les équations fondamentales, le temps est renversable, c'est-à-dire que le changement de la variable temps t en -t laisse les équations fondamentales invariantes.

Ainsi pour la mécanique classique, « dérouler le film » d'une évolution physique à l'envers est tout à fait acceptable. Or cette vision heurte le bon sens et pour les phénomènes simples : un seul sens d'évolution est physiquement acceptable. Par exemple, une balle lâchée d'une certaine hauteur tombe au sol, y rebondit un certain temps puis s'arrête une fois qu'elle a cédé toute son énergie cinétique au sol. Pour la mécanique classique, il est tout à fait acceptable en théorie que le processus inverse se produise de façon spontanée : le sol fournirait alors de l'énergie à la balle, qui se mettrait à sauter de plus en plus haut jusqu'à retrouver la hauteur de la main qui l'a lâchée !

Néanmoins, les premiers succès historiques des Lois de Newton leur ont conféré longtemps un assise particulière dans le monde des sciences. Ainsi Laplace n'hésite pas à prédire, non seulement un déterminisme total des lois de la physique, mais également la possibilité, à partir d'un état donné de décrire le passé et le futur d'un système mécanique : le temps n'a pas de sens d'écoulement.

Un certain nombre de problèmes conceptuels et pratiques vont néanmoins se poser, essentiellement aux XVII^e siècle et XVIII^e siècles sous l'impulsion du développement des machines à vapeur notamment. Un des principaux problèmes est celui de la chaleur. Toutes les expériences montrent que celle-ci se transmet du corps chaud au corps froid, et ceci tant que les températures ne sont pas égales. Il est ainsi illusoire d'attendre que le corps froid cède de sa chaleur au corps chaud : une fois le transfert réalisé, il est irréversible. Une autre constatation cruciale de l'irréversibilité est la suivante : alors qu'il est extrêmement simple d'obtenir de la chaleur par un travail mécanique (c'est ainsi que nos ancêtres allumaient un feu, en frottant du bois sec) il apparaît beaucoup plus difficile de transformer ensuite cette même chaleur en travail (vous n'arriverez pas à faire bouger une baguette de bois sec en y mettant le feu par exemple). Il y a donc encore irréversibilité.

Néanmoins, même à cette époque, les tenants d'une approche mécaniste de la physique ont du mal à accepter la remise en cause de la réversibilité totale des évolutions. De grands physiciens comme Maxwell tentent de faire apparaître des paradoxes ou de mettre au point des expériences de pensée à même de contredire l'apparition de l'irréversibilité en physique (voir notamment la détente de Joule et Gay-Lussac et le Démon de Maxwell).

Phénomènes microscopiques et macroscopiques

Les problèmes résident dans l'approche microscopique ou particulaire de la mécanique classique où les objets étudiés sont des points matériels, ou bien des ensembles de points dont on oublie facilement la structure interne (comme pour le mouvement d'une planète dans le cosmos). A cette échelle et pour ce type d'objets étudiés individuellement, la physique semble réellement réversible. C'est la transition aux ensembles nombreux d'objets qui fait apparaitre le plus souvent les phénomènes irréversibles : c'est ce qu'on appelle le passage à la limite thermodynamique.

L'exemple le plus simple concerne les gaz. Alors qu'il est possible de déterminer un grand nombre de propriétés des gaz en considérant chaque particule comme ponctuelle et en utilisant exclusivement la mécanique classique^[2], toutes les transformations des gaz sont irréversibles, et la plupart d'entre elles inexplicables sans la thermodynamique.

Les explications théoriques qui permettent de comprendre l'irréversibilité d'une transformation appliquée à une multitude d'objets microscopiques en évolution individuelle réversible sont fournies par la physique statistique et la théorie du chaos.

L'irréversibilité thermodynamique

C'est la thermodynamique, qui interprète les phénomènes macroscopiques à partir de leurs causes microscopiques, qui permet un traitement rigoureux et complet des irréversibilités, en élargissant certains concepts de la mécanique classique (notamment celui d'énergie) et en lui adjoignant de nouveaux principes (Second principe de la thermodynamique).

Conditions d'irréversibilité

• inhomogénéités des grandeurs intensives,
• brutalité et rapidité de la transformation,
• présence de phénomènes dissipatifs.

Les transformations réelles sont irréversibles à cause notamment de phénomènes dissipatifs. Le système ne peut pas « revenir en arrière » de façon spontanée. En thermodynamique ceci est formalisée dans le cadre du second principe par un terme de création d'entropie qui caractérise le fait que le désordre global (système + environnement) augmente ou bien encore qu'une partie de l'information sur le système a été perdue. Il est tout à fait possible pour le système de retourner à un état immédiatement antérieur à une transformation irréversible, mais cela nécessite l'action d'un opérateur extérieur.

Expression et interprétation

L’expression moderne du second principe formalise cette création d’entropie et permet de quantifier l'irréversibilité d'une transformation. Pour tout système fermé, la variation d'entropie au cours d'une transformation peut s'écrire :

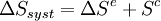
• Le terme 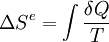correspond à l'entropie échangée entre le système et le milieu extérieur.

• Le terme 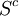est le terme de création d'entropie. Il est toujours positif et plus il est grand, plus la transformation du système étudié est irréversible. Dans le cas d'une transformation réversible (hypothétique), il est nul.

L'interprétation statistique de l'entropie et la théorie de l'information (avec notamment l'entropie de Shannon) fournissent également des interprétations à l'irréversibilité des transformations. Elle correspond :

• à une évolution spontanée de tous les systèmes vers l'uniformité ; quand toutes les grandeurs intensives décrivant le système sont uniformes, le système ne peut plus évoluer spontanément.

Exemple : quand un sucre se dissout dans une tasse de café, la concentration en sucre est initialement très hétérogène (infinie dans le sucre, nulle partout ailleurs), puis totalement homogène dans la tasse une fois que la dissolution a pris fin. La recomposition spontanée du morceau de sucre ne sera jamais observée.

• à une perte d'information sur l'état du système ; toutes les évolutions s'arrêtent lorsque le désordre du système est le plus grand possible.

Exemple : toujours lors de la dissolution du sucre, l'information sur l'état du système est celle-ci : le sucre est localisée dans le morceau, le café tout autour. A la fin de la transformation il est impossible de distinguer les localisations du sucre et du café, ce qui correspond à une perte d'information.

Remarques

• Au cours d'une transformation réelle, l'entropie d'un système peut diminuer mais il y a alors obligatoirement un transfert de chaleur et d'entropie vers le milieu extérieur. Néanmoins, le bilan entropique de l'ensemble (système + milieu extérieur) reste toujours positif. Exemple : lorsque l'eau gèle son entropie diminue (le solide glace est plus ordonné que l'eau liquide) mais ce phénomène s'accompagne d'un dégagement de chaleur (inverse de la chaleur de fusion). Il s'ensuit que l'entropie du milieu extérieur augmente et comme la transformation est irréversible le bilan entropique est positif.

Démontrons-le dans le cas d'un système composé d'un vase contenant de l'eau liquide que l'on place à l'air libre à -10 °C soit 263 K. L'eau gèle à 0 °C (273 K) et tant qu'il y a coexistence de glace et d'eau liquide cette température de changement d'état reste constante et égale à 273 K. La chaleur de solidification de l'eau L_(solid) est négative ainsi que l'entropie de solidification ΔS_(syst) = L_(solid) / 273 < 0. En revanche, la chaleur est reçue par le milieu extérieur dont la température n'est pas affectée par le système beaucoup plus petit. Elle reste constante et égale à 263 K. La variation d'entropie du milieu extérieur est alors égale à ΔS_(ext) = - L_(solid) / 263 > 0.

Calculons le bilan entropique :

ΔS_(syst) + ΔS_(ext) = ( L_(solid) / 273 ) + ( -L_(solid) / 263 ) = L_(solid) ( 1/273 - 1/263 ). Comme L_(solid) < 0, il s'ensuit que le bilan est positif et l'entropie créée sera d'autant plus grande que l'écart des températures sera grand ainsi que l'irréversibilité qui va de pair. Si la température du milieu extérieur était très proche de 273K à -ε près, on se rapprocherait d'une transformation réversible et le bilan entropique serait proche de zéro.

• Les transformations réelles sont irréversibles, donc l'entropie de l'univers ne peut qu'augmenter. Cette constatation est conforme avec la théorie de l'expansion de l'univers. En effet en augmentant de volume depuis le Big Bang, l'univers devient de plus en plus désordonné et donc son entropie augmente.

Transformation réversible

Les conditions théoriques d'une transformation réversible sont les suivantes :

• continuité des grandeurs intensives,
• lenteur (transformations quasi-statiques),
• absence de phénomènes dissipatifs.

De manière plus précise on peut dire qu'une transformation réversible est un modèle idéal pour lequel les échanges de grandeurs extensives sont quasistatiques, réalisés en un grand nombre d'étapes pour que le déséquilibre des grandeurs intensives conjuguées^[3] soit réalisé par pas très faibles, et en l'absence de phénomènes dissipatifs. Il est très souvent possible, dans des conditions expérimentales adéquates, de se rapprocher de ce modèle.

Application au calcul du travail des forces de pression

Considérons la transformation isotherme réversible d’un gaz parfait partant d’un état initial A défini par les variables d'état : p(A), V(A), T, n pour aboutir à l’état final d’équilibre B défini par : p(B), V(B), T, n.

L’expression élémentaire du travail des forces de pression est : .

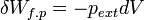Si la transformation est réversible le déséquilibre entre la pression extérieure p_ext et la pression du gaz p est très faible pendant toute la transformation, donc p_ext ≈ p. De plus à chaque instant le système est à l’équilibre et peut être décrit par son Équation d'état. Si le gaz est parfait :

• 

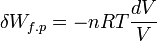
Le travail effectué au cours de la transformation correspond à l’intégrale définie pour une variation de volume entre V(A) et V(B) .

• 

Ce calcul n’est possible que si la transformation est réversible. Le travail obtenu dépend ici de la façon de procéder à la transformation.

Exemples

Cycle compression-détente d'un gaz

Transfert thermique

Soit un corps solide de capacité thermique constante c, et de température initiale T. Son énergie interne est U(T) = c T et son entropie S(T) = c Ln T. Ce corps est mis en contact avec une source de température T' = x T. Sa température finale à l'équilibre sera donc T' et il aura échangé avec la source la chaleur Q = c (T'-T) = c T (x-1).

Étude de la variation d'entropie

On a, entre l'état initial et l'état final, la variation d'entropie suivante :

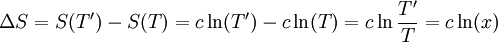
L'entropie échangée avec la source à la température T' est par définition :

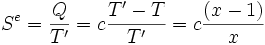
L'entropie créée S^c au cours de la transformation est donc, selon le second principe :

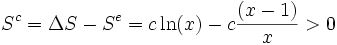
L'évolution est donc toujours irréversible, quelles que soient les températures finale et initiale.

Transformation quasi-statique

On imagine maintenant une transformation menant encore le corps solide de la même température initiale T à la même température finale T’ mais en mettant le corps successivement en contact avec une série de i sources de chaleur à des températures s'échelonnant graduellement de T à T'.

S étant une fonction d'état qui ne dépend que des conditions initiales et finales, la variation d'entropie reste inchangée :

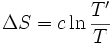
L'entropie échangée par le corps avec la source de chaleur i, à la température Tⁱ est égale à :

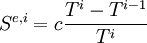
Si on considère que la transformation est réalisée de manière quasistatique, le nombre d'étapes, c'est-à-dire i, tend vers l'infini. Dans ce cas la différence de température (Tⁱ − T^{i − 1}) est infiniment petite et on pose dTⁱ = Tⁱ − T^{i − 1}.

L'entropie échangée totale par le corps est la somme des entropies échangées avec chacune des sources :

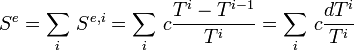
Pour i tendant vers l'infini et pour les température extrêmes T et T' on a :

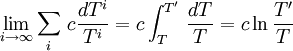
Et finalement, on trouve pour cette transformation quasi-statique une entropie créée limite :

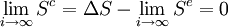
donc que la transformation tend à être réversible^[4] pour une transformation quasi-statique.

Expérience de Joule quasistatique

Interprétation microscopique

Frottement de Coulomb

Les phénomènes à hystérésis

• aimantation ...

Couplages linéaires de phénomènes irréversibles

L'irréversibilité en mécanique quantique

Irréversibilité et apparition de structure organisée

• Citer Ilya Prigogine et Isabelle Stengers

Irréversibilité en thermochimie

En thermochimie, la notion d'irréversibilité est aussi présente de façon majeure. En effet, aucune transformation chimique n'est réversible, et l'entropie créée sera toujours strictement positive. Cela provient du fait que tout système physico-chimique évolue vers un état d'équilibre dans lequel la réaction chimique sera compensée par la réaction inverse ( sauf dans le cas d'une rupture d'équilibre obtenue par exemple, soit en régénérant un réactif de départ, soit en éliminant au fur et à mesure qu'il se forme, un produit de la réaction...). Avant d'aboutir à cet équilibre, les composants du système sont dans un état moins stable, et on ne peut imaginer que le système réactionnel revienne à l'état initial, sans une intervention du milieu extérieur.

Notes et références

Voir aussi

Articles connexes

• The Animate and the Inanimate
• William James Sidis
• Onde de choc
• Irréversibilité en chimie
• Exemples de calculs d'entropie

Liens externes

Bibliographie

• Portail de la physique
• Portail de la chimie