Élagage alpha-beta

Élagage alpha-beta

L'élagage alpha-beta est une technique permettant de réduire le nombre de nœuds évalués par l'algorithme minimax.

L'algorithme minimax effectue en effet une exploration complète de l'arbre de recherche jusqu'à un niveau donné, alors qu'une exploration partielle de l'arbre est généralement suffisante : lors de l'exploration, il n'est pas nécessaire d'examiner les sous-arbres qui conduisent à des configurations dont la valeur ne contribuera sûrement pas au calcul du gain à la racine de l'arbre. L’élagage αβ nous permet de réaliser ceci.

Plus simplement, l'élagage αβ évite d'évaluer des nœuds dont on est sûr que leur qualité sera inférieure à un nœud déjà évalué, il permet donc d'optimiser grandement l'algorithme minimax sans en modifier le résultat.

Il est très utilisé dans le cas de jeux à 2 joueurs, comme par exemple les échecs ou les dames.

Principe

On prend α et β appartenant au domaine d’arrivée de la fonction d’évaluation tel que α < β. On définit la fonction AlphaBeta ainsi :

• AlphaBeta(P, α, β) = g(P) si P est une feuille de l'arbre et g la fonction d'évaluation du nœud
• AlphaBeta(P, α, β) = min(β, max(-AlphaBeta(O_i, -β, -α))) où les O_i sont les fils du nœud P

On appelle fenêtre αβ le couple (α, β) où α et β sont les deux paramètres d’appel de la fonction. Les nœuds élagués sont ceux qui seraient appelés avec une fenêtre tel que α ≥ β. Il existe 3 types de nœuds ne pouvant donc pas être élagués :

• Nœud de type 1 : fenêtre d’appel : (-∞, +∞)
• Nœud de type 2 : fenêtre d’appel : (-∞, β) avec β ≠ +∞
• Nœud de type 3 : fenêtre d’appel : (α, +∞) avec α ≠ -∞

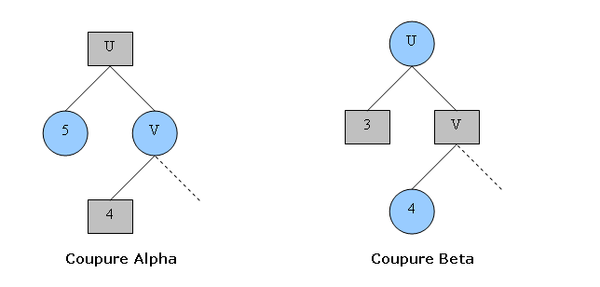
Le schéma ci-dessus présente les deux types de coupures possibles. Les nœuds Min sont représentés par un rond bleu et les nœuds Max par un carré gris. Rappel : les nœuds Min prennent la valeur minimum de leurs fils (et respectivement maximum pour les nœuds Max).

Coupure Alpha : le premier fils du nœud Min V vaut 4 donc V vaudra au plus 4. Le nœud Max U prendra donc la valeur 5 (maximum entre 5 et une valeur inférieure ou égale à 4).

Coupure Beta : le premier fils du nœud Max V vaut 4 donc V vaudra au minimum 4. Le nœud Min U prendra donc la valeur 3 (minimum entre 3 et une valeur supérieure ou égale à 4).

Pseudocode

Ci-dessous une implémentation en pseudocode de l'algorithme alpha-beta : alpha est initialisé à -INFINI et beta à +INFINI

fonction ALPHABETA(P, alpha, beta) /* alpha est toujours inférieur à beta */
   si P est une feuille alors
       retourner la valeur de P
   sinon
       si P est un nœud Min alors
           Val = infini
           pour tout fils Pi de P faire
               Val = Min(Val, ALPHABETA(Pi, alpha, beta))                
               si alpha ≥ Val alors  /* coupure alpha */
                   retourner Val
               beta = Min(beta, Val)
           finpour            
       sinon
           Val = -infini
           pour tout fils Pi de P faire
               Val = Max(Val, ALPHABETA(Pi, alpha, beta))                
               si Val ≥ beta alors /* coupure beta */
                   retourner Val
               alpha = Max(alpha, Val)
           finpour
       finsi
   retourner Val
   finsi
fin

De la même manière que l'algorithme minimax peut être remplacé par NegaMax, on simplifie Alpha-Beta. Cela donne l’algorithme suivant :

fonction ALPHABETA(P, A, B) /* A < B */
   si P est une feuille alors
       retourner la valeur de P
   sinon
       Meilleur = –INFINI
       pour tout fils Pi de P faire
           Val = -ALPHABETA(Pi,-B,-A)
           si Val > Meilleur alors
               Meilleur = Val
               si Meilleur > A alors
                   A = Meilleur
                   si A ≥ B alors
                       retourner Meilleur
               finsi
           finsi
       finpour 
       retourner Meilleur
   finsi
fin

Exemple

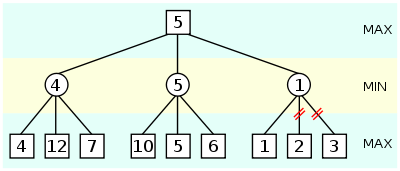
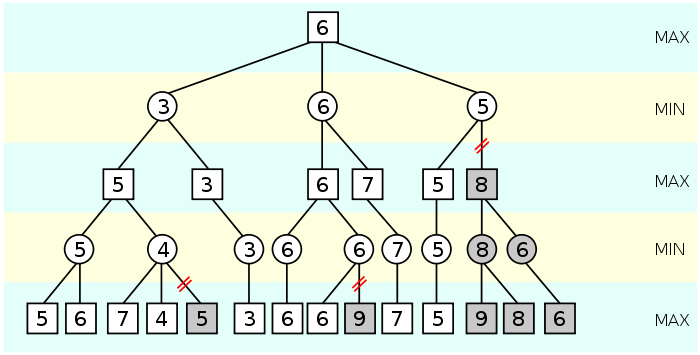
Nous allons illustrer l’algorithme sur l’arbre ci-dessous déjà étiqueté avec les valeurs d’un minimax. Le résultat obtenu est le schéma ci-dessous.

Minimax avec élagage alpha-beta

Plusieurs coupures ont pu être réalisées :

1. Le nœud MIN vient de mettre à jour sa valeur courante à 4. Celle-ci, qui ne peut que baisser, est déjà inférieure à α=5, la valeur actuelle du nœud MAX précédent. Celui-ci cherchant la valeur la plus grande possible, ne la choisira donc de toute façon pas.
2. Le nœud MIN vient de mettre à jour sa valeur courante à 6. Celle-ci, qui ne peut que baisser, est déjà égale à α=6, la valeur actuelle du nœud MAX précédent. Celui-ci cherchant une valeur supérieure, il ne mettra de toute façon pas à jour sa valeur que ce nœud vaille 6 ou moins.
3. Le nœud MIN vient de mettre à jour sa valeur courante à 5. Celle-ci, qui ne peut que baisser, est déjà inférieure à α=6, la valeur actuelle du nœud MAX précédent. Celui-ci cherchant la valeur la plus grande possible, ne la choisira donc de toute façon pas.

Voir aussi

• Séparation et évaluation

Lien externe

• Tristan Cazenave, « Des optimisations de l'Alpha-Beta », dans Actes du colloque de Berder, 2000 [texte intégral [PDF] (page consultée le 7 mai 2010)] 

• Portail de l’informatique
• Portail de l'informatique théorique