²

En mathématiques, le carré d'un nombre désigne une valeur, égal au nombre initial multiplié par lui-même. De manière plus générale, tout être mathématique sur lequel il existe une multiplication possède un carré. Ainsi, on parle de carré d'une matrice ou encore d'une fonction.

La fonction carré désigne celle qui, à un nombre donné associe son carré. Cette fonction est paire, c'est-à-dire que l'image d'une valeur ou de son opposée est la même. Le carré de 4 ou de -4 est égal à 16. Le carré d'un nombre réel est toujours un nombre positif et, comme les nombres entiers ou rationnels sont aussi des nombres réels, leurs carrés sont aussi positifs.

Tout nombre réel strictement positif est le carré d'exactement deux nombres, l'un strictement positif l'autre strictement négatif, 0 est uniquement le carré de lui même. Pour cette raison, il est possible de définition une fonction racine carrée, qui à un nombre réel, associe le nombre positif dont le carré est le nombre initial. La situation est un peu différente pour les nombres entiers, un entier positif n'est pas nécessairement le carré d'un autre nombre entier. La valeur 4 l'est, car 2x2 est égal à 4, mais 2 ne l'est pas. Un nombre entier qui est un carré est dit carré parfait.

Le terme de carré s'est imposé à une époque où la logique de l'algèbre géométrique était omniprésente. Un nombre était toujours positif et correspondait à la longueur d'un segment. Le carré de ce nombre était vu comme l'aire d'un carré de coté la longueur initiale.

Exemples :

• 5² = 25
• 1² = 1
• 10² = 100
• 

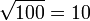
Sommaire 1 Généralités sur le carré 2 La racine carrée 3 Résoudre l'équation x² = a dans l'ensemble des réels 3.1 Premier cas : a < 0 3.2 Deuxième cas : a = 0 3.3 Troisième cas : a > 0 4 Notes et références de l'article 5 Voir aussi

Généralités sur le carré

Quand on calcule le carré d'un nombre, on le multiplie par lui-même. Ainsi, les formes 12² et 12 x 12 sont équivalentes. Néanmoins on préfère la forme 12² autant que possible pour sa clarté et sa concision. Un carré est toujours positif pour tout nombre réel.

Exemple : 12² = (-12)² = 12 x 12 = -12 x (-12) = 144

Attention ! -(12²) et (-12)² sont deux nombres différents. Le premier vaut -144 (on multiplie 12 par 12 puis par -1) et le deuxième 144 (le - est englobé dans la parenthèse).

La racine carrée

Comme on peut élever un nombre au carré, on peut aussi faire l'opération inverse. Notons que le symbole 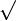s'appelle le "radical". Cela s'appelle la racine carrée d'un nombre. Soit a un nombre positif, la racine carrée de a s'écrit : 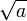Il est important de préciser que a doit être positif. En effet écrire 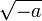par exemple reviendrait à dire que a² < 0 ce qui n'est pas possible dans l'ensemble des réels. Par contre, comme il est possible d'écrire -(12²) il est tout à fait possible d'écrire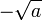

Résoudre l'équation x² = a dans l'ensemble des réels

x²=a²/b²

Premier cas : a < 0

Lorsque a est strictement inférieur à 0, cela revient à dire que x² est négatif. Or dans l'ensemble des réels, le carré d'un nombre n'est jamais négatif. Donc :

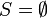
Deuxième cas : a = 0

Lorsque a vaut 0, une seule solution est possible : 0 (puisque zéro n'a pas de signe). Donc :

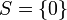
Troisième cas : a > 0

Nous avons vu dans la partie précédente que 12² = (-12)² = 144. On peut réappliquer cette affirmation à l'équation x² = a. Ici l'équation a donc deux solutions :

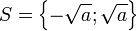
Remarque : résoudre

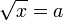
Si a est strictement négatif, l'équation n'a pas de solution. Donc :

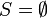
Par contre si 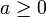alors trouver x revient à multiplier a par lui-même, c'est-à-dire a².

Notes et références de l'article

Source principale de cet article : cours de mathématiques niveau 3ème/2nde

Voir aussi

• Fonction carré
• Puissance (mathématiques élémentaires)
• Racine carrée
• Pour aller plus loin : Racine cubique

• Portail des mathématiques