Valuation de Krull

Valuation de Krull

Valuation de Krull

En algèbre, une valuation de Krull est une extension de la notion de valeur absolue non archimédienne. Sur un corps (commutatif) K, une valuation de Krull est une application 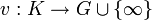v:K\rightarrow G\cup \{\infty\}, où G est un groupe abélien totalement ordonné, vérifiant les trois propriétés suivantes :

  • Pour tout x, 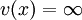v(x)=\infty ssi x=0 ;
  • Pour tous x et y dans K, v(xy) = v(x) + v(y) ;
  • Pour tous x et y dans K, v(x+y)\geq min[v(x),v(y)].

La première propriété implique que la restriction de v à K * définit une application 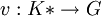v:K*\rightarrow G. La deuxième propriété dit exactement que cette application est un morphisme de groupes. L'image est un sous-groupe de G. Par corestriction, on peut toujours supposer v surjective. À v est associée la plus petite topologie sur K rendant v continue pour la topologie de l'ordre sur G.

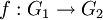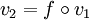Deux valuations de Krull surjectives v1 et v2 sont dites équivalentes lorsqu'il existe un isomorphisme de groupes ordonnés f:G_1\rightarrow G_2 tel que : v_2=f\circ v_1.

Si G est un sous-groupe de R, alors, exp( − v) est une valeur absolue non-archimédienne (les vérifications étant immédiates). L'équivalence entre deux telles valuations équivaut à l'équivalence entre les valeurs absolues associées.

Pour une valuation de Krull v sur K, l'ensemble A des x pour lesquels 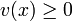v(x)\geq 0 est un sous-anneau de K, qui se trouve être un anneau de valuation. On dispose ainsi d'une bijection entre les classes d'équivalence de valuations de Krull surjectives et les anneaux de valuation de K.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Valuation de Krull ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Valuation de Krull de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Valuation de krull — En algèbre, une valuation de Krull est une extension de la notion de valeur absolue non archimédienne. Sur un corps (commutatif) K, une valuation de Krull est une application , où G est un groupe abélien totalement ordonné, vérifiant les trois… …   Wikipédia en Français

  • Valuation — En mathématiques, plus particulièrement en géométrie algébrique et en théorie des nombres, une valuation, ou valuation de Krull, est une mesure de la multiplicité. La notion est une généralisation de la notion de degré ou d ordre d annulation d… …   Wikipédia en Français

  • Krull dimension — In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull (1899–1971), is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring. A… …   Wikipedia

  • Krull ring — A Krull ring is a particular type of commutative ring studied in commutative algebra and related branches of mathematics and named after the German mathematician Wolfgang Krull.Formal definitionLet A be an integral domain and let P be the set of… …   Wikipedia

  • Discrete valuation ring — In abstract algebra, a discrete valuation ring (DVR) is a principal ideal domain (PID) with exactly one non zero maximal ideal. This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions: R is a local… …   Wikipedia

  • Anneau de valuation discrète — En mathématiques, plus précisément en algèbre commutative, un anneau de valuation discrète est un anneau de valuation dont la valuation est discrète mais non triviale. Un anneau est de valuation discrète lorsqu il est principal, qu il ne possède… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Local ring — In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called local behaviour , in the sense of functions defined on varieties or manifolds, or of… …   Wikipedia

  • Regular local ring — In commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is exactly the same as its Krull dimension. The minimal number of generators of the maximal… …   Wikipedia

  • Serial module — Chain ring redirects here. For the bicycle part, see Chainring. In abstract algebra, a uniserial module M is a module over a ring R, whose submodules are totally ordered by inclusion. This means simply that for any two submodules N1 and N2 of M,… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”