Univers de de sitter

Univers de de sitter

Univers de de Sitter

L'univers de de Sitter est une solution exacte des équations de la relativité générale correspondant physiquement à un univers homogène, isotrope, vide de matière mais rempli d'une constante cosmologique positive et notée ici Λ. C'est un espace de courbure positive (valant 4Λ) bien que sa courbure spatiale puisse être quelconque. Il porte le nom du physicien Willem de Sitter.

Il entre dans la classe générale de solutions de type Friedmann-Lemaître-Robertson-Walker. Le facteur d'échelle correspondant à cette géométrie est, en notant k la courbure spatiale valant 1 (resp. 0 ou -1) si la courbure spatiale est positive (resp. nulle ou négative).


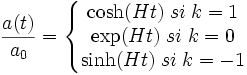
\frac{a(t)}{a_0}=\left\{\begin{matrix} \cosh(Ht) \; si \; k=1\\ \exp(Ht) \; si \; k=0\\ \sinh(Ht) \; si \; k=-1\\ \end{matrix} \right.

où H est le taux d'expansion ou paramètre de Hubble et est ici constant. Il est relié à la constante cosmologique par la relation.

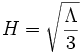
H=\sqrt{{\Lambda\over 3}}

On voit que pour les temps longs, Ht > > 1, la distinction entre les différentes courbures spatiales disparaît. En réalité, ces trois solutions apparemment différentes peuvent être vues comme trois systèmes de coordonnées différents du même espace quadridimensionnel (voir espace de Sitter pour plus de détails mathématiques sur ce fait). Ceci tient à l'ambiguïté, du point de vue de l'espace total à quatre dimensions, de la séparation faite entre la coordonnée de temps qui joue le rôle de temps cosmique et des trois coordonnées spatiales.

Dans un univers de de Sitter la distance entre observateurs comobiles croît si vite qu'il n'est pas possible pour un observateur de détecter quoi que ce soit au-delà d'une distance cH − 1 appelée horizon particulaire. De même un événement ne peut pas avoir d'influence en tout lieu situé au-delà d'une distance cH − 1 et on parle dans ce cas d'horizon des événements.

L'univers de de Sitter est le prototype des géométries apparaissant dans le cadre de l'inflation cosmique. Dans ces scénarios la valeur de la constante de Hubble H n'est pas donnée par une constante cosmologique mais dépend de la valeur d'un champ appelé inflaton. Elle est approximativement constante pendant une courte période suivant le Big Bang aboutissant ainsi à une géométrie effectivement de Sitter pendant ce laps de temps.

Voir aussi

Quelques modèles cosmologiques
Atome primitif • Big Bang • Big Crunch • Big Rip • Classification de Bianchi • Cosmologie branaire • Cosmologie cordiste • Dimensions supplémentaires • Espace anti de Sitter • Espace de Sitter • Espace de Taub-NUT • Inflation cosmique • Modèle ΛCDM • Modèle cyclique • Modèle OCDM • Modèle SCDM • Modèle standard de la cosmologie • Pré Big Bang • Théorie de l'état stationnaire • Univers d'Einstein • Univers de Friedmann-Lemaître-Robertson-Walker • Univers de Gödel • Univers de Milne • Univers de de Sitter • Univers ekpyrotique • Univers en tore bidimensionnel • Univers fractal • Univers hésitant • Univers mixmaster • Univers phénix
  • Portail de la cosmologie Portail de la cosmologie
Ce document provient de « Univers de de Sitter ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Univers de de sitter de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Univers anti de sitter — L univers anti de Sitter est un modèle cosmologique dans lequel le contenu matériel de l univers est exclusivement composé d une constante cosmologique de valeur négative. Le nom d anti de Sitter résulte du fait qu il forme en un certain sens le… …   Wikipédia en Français

  • Univers de de Sitter — L univers de de Sitter est une solution exacte des équations de la relativité générale correspondant physiquement à un univers homogène, isotrope, vide de matière mais rempli d une constante cosmologique positive et notée ici Λ. C est un espace… …   Wikipédia en Français

  • Univers anti de Sitter — L univers anti de Sitter est un modèle cosmologique dans lequel le contenu matériel de l univers est exclusivement composé d une constante cosmologique de valeur négative. Le nom d anti de Sitter résulte du fait qu il forme en un certain sens le… …   Wikipédia en Français

  • Univers de Sitter — Univers de de Sitter L univers de de Sitter est une solution exacte des équations de la relativité générale correspondant physiquement à un univers homogène, isotrope, vide de matière mais rempli d une constante cosmologique positive et notée ici …   Wikipédia en Français

  • Univers hesitant — Univers hésitant Le terme d’univers hésitant se réfère à un modèle cosmologique décrivant un univers homogène et isotrope c’est à dire de type Friedmann Lemaître Robertson Walker dont l’expansion passe dans un premier temps par une phase… …   Wikipédia en Français

  • Univers fini de friedmann — Parmi les nombreux modèles cosmologiques de notre Univers, le modèle d’univers fini de Friedmann occupe une place à part parce qu il est historiquement l un des premiers à avoir fourni une image physiquement cohérente du cosmos dans le cadre de… …   Wikipédia en Français

  • Univers d’Einstein — Univers d Einstein L univers d Einstein est le nom qui a été donné au premier modèle cosmologique basé sur la théorie de la relativité générale découverte par Albert Einstein en 1915. Le modèle a été proposé par Einstein lui même en 1917, mais a… …   Wikipédia en Français

  • Univers de milne — Chronologie du Modèle standard de la cosmologie Cosmologie quantique (?) Ère de Planck (?) Inflation cosmique Préchauffage Réchauffage Ère d …   Wikipédia en Français

  • Univers de Godel — Univers de Gödel L univers de Gödel est une solution aux équations de la relativité générale publiée par le mathématicien Kurt Gödel en 1949. Sommaire 1 Description 2 Métrique de l univers de Gödel 3 Propriétés …   Wikipédia en Français

  • Univers de gödel — L univers de Gödel est une solution aux équations de la relativité générale publiée par le mathématicien Kurt Gödel en 1949. Sommaire 1 Description 2 Métrique de l univers de Gödel 3 Propriétés …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”