- Triangulation d'un polygone
-
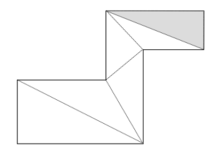
En géométrie algorithmique, la triangulation d'un polygone consiste à décomposer ce polygone en un ensemble (fini) de triangles[1].
Une triangulation d'un polygone P est une partition de P en un ensemble de triangles qui ne se recouvrent pas, et dont l'union est P. Dans le cas le plus restrictif, on impose que les sommets des triangles ne soient que les sommets de P. Dans un cadre plus permissif, on peut rajouter des sommets à l'intérieur de P ou sur la frontière pour servir de sommets aux triangles.
Les triangulations sont des cas particuliers de graphes planaires rectilignes (i.e. dont les arêtes sont des segments).
La triangulation d'un polygone convexe est triviale et se calcule en un temps linéaire, par exemple en partant d'un sommet et en ajoutant des arêtes avec tous les autres sommets. En 1991, Bernard Chazelle (en) montra que tout polygone simple peut être triangulé en un temps linéaire[2]. L'algorithme proposé est cependant très complexe, et des algorithmes plus simples sont toujours recherchés.
Sommaire
Méthodes de résolution
Méthode "des oreilles"
Une manière de trianguler un polygone simple est d'utiliser le fait que tout polygone simple sans trou possède au moins deux "oreilles"[3]. Une oreille est un triangle avec deux arêtes appartenant à la frontière du polygone, et la troisième située à l'intérieur du polygone. L'algorithme consiste à trouver une telle oreille, à la retirer du polygone, ce qui donne un nouveau polygone qui répond toujours aux conditions, et à répéter l'opération jusqu'à ce qu'il n'y ait plus qu'un seul triangle.
Cet algorithme est simple à implémenter, mais sous-optimal : une implémentation qui stocke des listes séparées de sommets pour les triangles et le polygone aura une complexité en O(n²). De plus, il ne fonctionne que sur des polygones sans trous.
Décomposition en chaînes monotones
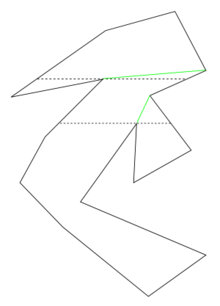
Un polygone monotone est tel que sa frontière peut être divisée en deux parties, chacune d'entre elle étant composée de points dont les coordonnées selon une dimension donnée ne font que croître : la frontière ne revient pas "en arrière". A. Fournier et D. Y. Montuno ont montré qu'un tel polygone peut être triangulé en temps linéaire[4].
Pour diviser un polygone en polygones monotones, on utilise une ligne verticale ou horizontale qui balaie les coordonnées dans une direction[1].
Cet algorithme a une complexité en O(n log n).
Notes et références
Notes
- (en) Mark de Berg, Marc van Kreveld, Mark Overmars et Otfried Schwarzkopf, Computational Geometry, Springer Verlag, 2000, 2e éd. (ISBN 3-540-65620-0), chap. 3 (« Polygon Triangulation »), p. 45-61
- (en) Bernard Chazelle, « Triangulating a Simple Polygon in Linear Time », dans Discrete & Computational Geometry, vol. 6, 1991, p. 485–524 (ISSN 0179-5376) [lien DOI]
- (en) Gary Hosler Meisters, « Polygons have ears », dans American Mathematical Monthly, vol. 82, 1975, p. 648-651 [texte intégral (page consultée le 11 octobre 2010)]
- (en) A. Fournier et D. Y. Montuno, « Triangulating simple polygons and equivalent problems », dans ACM Transactions on Graphics, vol. 3, no 2, avril 1984, p. 153–174 (ISSN 0730-0301) [lien DOI]
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Polygon triangulation » (voir la liste des auteurs)
- (en) Nancy M. Amato, Michael T. Goodrich et Edgar A. Ramos, « A Randomized Algorithm for Triangulating a Simple Polygon in Linear Time », dans Discrete & Computational Geometry, vol. 26, 2000, p. 245–265 (ISSN 0179-5376) [texte intégral, lien DOI]
Articles connexes
Catégories :- Algorithme géométrique
- Polygone
- Graphe géométrique
Wikimedia Foundation. 2010.