Transition berezinsky-kosterlitz-thouless

Transition berezinsky-kosterlitz-thouless

Transition Berezinsky-Kosterlitz-Thouless

En physique théorique la transition de Berezinky-Kosterlitz-Thouless est une transition de phase obtenue dans le modèle XY à deux dimensions (ou modèle planaire) en variant la température.

Sommaire

La transition BKT

Dans la phase de basse température, l'interaction premier voisins entre les moments magnétiques du modèle planaire, − Jcos(φi − φj) peut être approchée par une interaction quadratique K(φi − φj)2, et le modèle planaire est alors équivalent au modèle Gaussien. Il en résulte une décroissance en loi de puissance des fonctions de corrélations 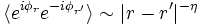\langle e^{i \phi_r} e^{-i \phi_{r'}}\rangle \sim |r-r'|^{-\eta} où l'exposant η est proportionel à la température. ...

Dans la phase de haute température, la périodicité de 2π de l'interaction redevient importante, et l'approximation gaussienne doit être corrigée. Plus précisément, si on considère la somme des différences angulaires entre premier voisins φi − φj sur un circuit fermé, on remarque que la périodicité impose seulement que cette somme doit valoir un nombre entier de fois 2π. Partant de cette remarque, Kosterlitz et Thouless en 1973 (et indépendamment Berezinsky en 1972) ont ajouté à l'approximation gaussienne des solutions singulières de l'équation de Laplace discrète, telles qu'il existe des points autour desquels la somme des différences angulaires sur un circuit fermé soit égal à un nombre entier non nul q multiplié par 2π. Ces points sont appelés des vortex, et q est appelé la charge topologique du vortex.

L'énergie des configurations considérées par Kosterlitz et Thouless peut s'écrire comme une somme d'énergies d'interaction à deux corps entre les vortex proportionnelles au produit des deux charges topologiques et proportionnelle au logarithme de la distance entre les vortex. Cette expression est identique à l'énergie d'interaction électrostatique par unité de longueur de fils infinis portant une densité linéique de charge proportionnelle à la charge topologique du vortex. La transition de Kosterlitz-Thouless peut donc être vue comme une transition de phase dans un gaz de Coulomb bidimensionnel.

Dans la phase de basse température, les vortex sont confinés en paires de vortex de charge opposées. Pour le gaz de Coulomb, il n'y a pas de charge libre mais seulement des dipôle magnétiques, et la constante diélectrique est finie.

Dans la phase de haute température les vortex sont libres et font décroître exponentiellement les fonctions de corrélation : 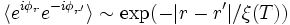\langle e^{i \phi_r} e^{-i \phi_{r'}}\rangle \sim \exp(-|r-r'|/\xi(T)). ξ(T) est appelée la longueur de corrélation. En utilisant le groupe de renormalisation, Kosterlitz et Thouless ont montré que \xi(T) \sim \exp\left[-\left(\frac{T_{BKT}}{T-T_{BKT}}\right)^{1/2}\right]. Pour le gaz de Coulomb, cela signifie qu'il existe des charges libres, et que dans la phase de haute température le gaz de Coulomb devient un plasma avec une constante diélectrique infinie. La longueur de corrélation s'interprète alors comme une longueur d'écrantage de Debye-Huckel : au delà de la longueur ξ(T) l'interaction effective entre deux vortex est nulle.

La transition de Kosterlitz-Thouless se distingue des transitions de phase conventionnelles sur plusieurs points :

  1. Absence de paramètre d'ordre : aucune symétrie globale n'est brisée à la transition. On observe juste un changement du comportement qualitatif des fonctions de corrélation.
  2. Absence de chaleur latente (contrairement à la transition liquide-gaz) et absence de singularité en loi de puissance de chaleur spécifique (contrairement à la transition de Curie d'un ferromagnétique). Dans la classification d'Ehrenfest des transitions de phase, la transition de Kosterlitz-Thouless est une transition d'ordre infini.
  3. Existence d'une ligne de points critiques pour T < TBKT avec des exposants critiques qui varient continument avec la température. Le comportement critique n'est pas universel.

Autres modèles et généralisations

Outre le modèle planaire, il existe d'autres modèles bidimensionnels qui possèdent une transition de Berezinsky-Kosterlitz-Thouless. En particulier, certains modèles exactement solubles étudiés par Rodney Baxter, comme le modèle à 6 vertex, possèdent une ligne de points critiques qui se termine par une transition de Berezinsky-Kosterlitz-Thouless. D'autre part, il existe des modèles quantiques unidimensionnels tels que la chaine de spin 1/2 antiferromagnétique anisotrope (modèle XXZ) qui possèdent une transition de Berezinsky-Kosterlitz-Thouless entre une phase Liquide de Luttinger et une phase de Néel.

Ces modèles peuvent etre ramenés au modèle à 6 vertex par des techniques de matrice de transfert. Enfin, Kosterlitz, Thouless, Halperin, Nelson et Young (KTHNY) ont proposé en 1979 une généralisation de la transition de Berezinsky-Kosterlitz-Thouless décrivant la fusion d'un cristal bidimensionnel. Les vortex sont y remplacés par les dislocations du cristal. Celles ci possédent une charge vectorielle qui est leur vecteur de Burgers. Dans la phase de basse température, les dislocations sont liées, et le cristal possède un quasi-ordre à longue distance. Dans la phase de haute température les dislocations sont libres, et le quasi-ordre est détruit. On obtient un liquide qui possède encore un ordre orientationnel. Cet ordre orientationnel est détruit à plus haute température par la formation de disinclinaisons.

Expériences visant à mettre en évidence la transition de BKT

Du point de vue expérimental, comme la transition superfluide-normal ou la transition supraconducteur-métal normal sont dans la classe d'universalité du modèle XY, des expériences ont été faites sur des films d'hélium 4 et des films supraconducteurs pour mettre en évidence cette transition. La théorie de Kosterlitz-Thouless prédit un saut universel de la densité superfluide à la transition qui a été mis en évidence dans des expériences de J. D. Reppy sur des films d'hélium (Physical Review Letters, 1978).

En ce qui concerne la théorie KTHNY, la situation expérimentale est moins nette, certaines expériences donnant apparemment une transition non-conventionnelle, d'autre produisant une transition du premier ordre avec chaleur latente. En général, il semble que la théorie KTHNY décrit bien la fusion des cristaux liquides smectiques.

Références

  • C. Itzykson et J. M. Drouffe Théorie Statistique des Champs, vol. I (CNRS-Interéditions)
  • M. Le Bellac Des phénomènes critiques aux champs de jauge (CNRS-Interéditions)
  • Katherine J. Strandburg "Two-Dimensional Melting" Rev. Mod. Phys. 60, 000161 (1988)
  • D. E. Angelescu et al. "Two-Dimensional Melting Transition Observed in a Block Copolymer" Phys. Rev. Lett. 95, 025702 (2005)
  • Kosterlitz J. M. et Thouless D. J. "Ordering, metastability and phase transitions in two-dimensional systems" J. Phys. C: Solid State Phys. 6, 1180 (1973)
  • Portail de la physique Portail de la physique
Ce document provient de « Transition Berezinsky-Kosterlitz-Thouless ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transition berezinsky-kosterlitz-thouless de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Transition Berezinsky-Kosterlitz-Thouless — En physique théorique la transition de Berezinky Kosterlitz Thouless est une transition de phase obtenue dans le modèle XY à deux dimensions (ou modèle planaire) en variant la température. Sommaire 1 La transition BKT 2 Autres modèles et… …   Wikipédia en Français

  • Kosterlitz–Thouless transition — The Kosterlitz–Thouless transition, or Berezinsky–Kosterlitz–Thouless transition, is a special transition seen in the XY model for interacting spin systems in 2 spatial dimensions.The XY model is a 2 Dimensional vector spin model that possesses… …   Wikipedia

  • Transition de phase — En physique, une transition de phase est une transformation du système étudié provoquée par la variation d un paramètre extérieur particulier (température, champ magnétique...). Cette transition a lieu lorsque le paramètre atteint une valeur… …   Wikipédia en Français

  • Transition — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Transition », sur le Wiktionnaire (dictionnaire universel) en mathématiques : une matrice de… …   Wikipédia en Français

  • David J. Thouless — David James Thouless (born in 1934 in Bearsden, Scotland) is a condensed matter physicist and Wolf Prize winner. David James Thouless Born 1934 Bearsden, Scotland Residence …   Wikipedia

  • Seuil critique — Transition de phase En physique, une transition de phase est une transformation du système étudié provoquée par la variation d un paramètre extérieur particulier (température, champ magnétique...). Cette transition a lieu lorsque le paramètre… …   Wikipédia en Français

  • Transitions de phase — Transition de phase En physique, une transition de phase est une transformation du système étudié provoquée par la variation d un paramètre extérieur particulier (température, champ magnétique...). Cette transition a lieu lorsque le paramètre… …   Wikipédia en Français

  • Groupe De Renormalisation — En mécanique statistique, le groupe de renormalisation (qui est plutôt un semi groupe, les transformations n étant pas inversibles) est un ensemble de transformations qui permettent de transformer un hamiltonien en un autre hamiltonien par… …   Wikipédia en Français

  • Groupe de renormalisation — En mécanique statistique, le groupe de renormalisation (qui est plutôt un semi groupe, les transformations n étant pas inversibles) est un ensemble de transformations qui permettent de transformer un hamiltonien en un autre hamiltonien par… …   Wikipédia en Français

  • Modele XY — Modèle XY Pour les articles homonymes, voir XY. Le modèle XY ou modèle planaire est un modèle étudié en mécanique statistique. Il décrit un système dont les degrés de liberté sont des vecteurs bidimensionnels de norme unité placés aux nœuds d un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”