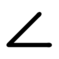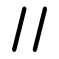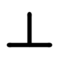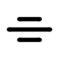Tolérances géométriques

En dessin technique, les tolérances géométriques, aussi appelés tolérances de forme et de position, ont pour objet la maîtrise de la géométrie de l'objet à fabriquer.

On parle aussi de spécification géométrique de produits, ou geometrical product specification, d'où le terme cotation GPS. On parle aussi de cotation ISO, la cotation étant définie par une série de normes ISO.

Sommaire 1 Utilité 2 Histoire des premières spécifications 3 Démarche 4 Exemple : perpendicularité d'un alésage 4.1 Du modèle de peau à l'objet idéal 4.2 Repère et zone de tolérance 5 Principes fondamentaux 5.1 Principe d'indépendance 5.2 Vocabulaire et opérations de base 5.3 Références 5.3.1 Référence primaire 5.3.2 Référence secondaire 5.3.3 Référence tertiaire 5.4 Exécution graphique de la cotation 6 Les différentes tolérances 6.1 Tolérances de forme 6.1.1 Ligne quelconque 6.1.2 Surface quelconque 6.1.3 Rectitude 6.1.4 Circularité 6.1.5 Planéité 6.1.6 Cylindricité 6.2 Tolérances d'orientation 6.2.1 Ligne quelconque 6.2.2 Surface quelconque 6.2.3 Inclinaison 6.2.4 Parallélisme 6.2.5 Perpendicularité 6.3 Tolérances de position 6.3.1 Ligne quelconque 6.3.2 Surface quelconque 6.3.3 Spécification de localisation 6.3.4 Coaxialité/concentricité 6.3.5 Symétrie 6.4 Tolérances de battement 6.4.1 Battement simple 6.4.2 Battement total 6.5 Exceptions au principe d'indépendance 6.5.1 Exigence de l'enveloppe 6.5.2 Exigence du maximum de matière 6.5.3 Exigence du minimum de matière 7 Notes 8 Voir aussi

Utilité

Une pièce est manufacturée pour remplir des fonctions. Certaines fonctions ne sont remplies que si la pièce a une forme définie, ce qui détermine la manière dont elle est conçue, dessinée. Cependant, l'objet réel, fabriqué, possède des défauts. La cotation fonctionnelle a pour but de définir les défauts acceptables.

Dans la cotation fonctionnelle, on distingue

• les tolérances dimensionnelles, qui déterminent les dimensions (longueur, largeur, rayon ou diamètre, …) ainsi que le jeu permettant le montage, le démontage et les mouvements ;
• les tolérances géométriques, étudiées ici.

La cotation GPS a pour but de lever les ambiguïtés sur les plans. En particulier, l'organisation de l'entreprise tend de plus en plus vers l'externalisation (recours à la sous-traitance) et l'internationalisation ; la personne qui doit interpréter le plan n'a donc pas nécessairement les mêmes habitudes que la personne qui l'a conçu. La mise en œuvre de la cotation GPS est surtout intéressante dans le contexte des grandes séries, en raison de la démarche à mettre en route, en particulier de formation des différents intervenants et de contrôle.

Histoire des premières spécifications

La notion d'interchangeabilité a été développée par le général français Jean-Baptiste de Gribeauval dès 1765. Un des intérêts à l’époque était de pouvoir échanger des pièces défectueuses de mousquets et de pistolets avec des pièces de remplacement récupérées sur d’autres pistolets sur le champ de bataille même. C’est à ce moment là que les notions de géométrie idéale et de réalisation imparfaite ont pris tout leur sens. Des méthodes ont été conçues pour contraindre les variations géométriques et les vérifier par des calibres entre/n’entre pas.

Le « principe de Taylor » apparaît sous la norme ISO/R 1938 de 1971, pour devenir ensuite le « principe d'enveloppe » qui vient de disparaître pour « l'exigence d'enveloppe » dans la dernière révision des normes ISO 8015 et ISO 286-1.

Au début des années 1990, un premier constat sur les normes relatives au tolérancement et à la métrologie révèle les lacunes et les contradictions. La raison provient des trois différentes instances en charges de ces questions, les instances :

• ISO/TC 3 « ajustement-métrologie » (Allemagne),
• ISO/TC 10/SC5 « cotation et tolérancement » (USA) et
• l'ISO/TC 57 « états de surface » (Russie).

Les normes sont développées au coup par coup sans une vision globale. Pour répondre à la continuité de la chaîne d'information du produit, de son opérateur de spécification à son opérateur de vérification, une première norme est élaborée établissant un schéma directeur des normes et des travaux à entreprendre, la norme FD CR ISO/TR 14638, décembre 1996 ^[1]. Cette norme met en place une matrice des chaînes de normes GPS générale, la matrice GPS. Dès lors, les normes ISO de spécification du produit deviennent des normes ISO-GPS. ^[2]

La normalisation est une activité essentiellement technique à vocation économique.

F. Contet, lors de la présentation du séminaire : Cotation ISO : les nouvelles normes, quelles conséquences ?.

Les normes en question sont^[3] :

• FD CR ISO/TR 14638 : 1996;
• ISO/DIS 14659 : 2007
• ISO TS 17450-1 : 2005 ;
• ISO TS 17450 -2 : 2004;
• ISO/FDIS 25378 :2007;
• ISO 14 660 -1 : 1999;
• ISO 14 660 -2 : 1999;
• ISO 8015 : 2006; (qui risque à court terme de disparaître, remplacé par l'ISO/FDIS 14405 :2006 et par l'ISO/DIS 14659 : 2007)
• ISO 3040 : 1990;
• ISO/FDIS 14405 :2006
• ISO/FDIS 5459 : 2005 ( des apports majeurs par rapport à la version de 1981);
• ISO 2692 : 2006 ( attention des modifications profondes par rapport à la version précédente);
• ISO 1101 : 2006 ;
• ISO 5458 : 1999 ( qui risque de disparaître par l'amendement à venir de l'ISO 1101);
• ISO 10578 : 1996 ( qui risque de disparaître par l'amendement à venir de l'ISO 1101);
• ISO 10579 : 1994 ( qui risque de disparaître par l'amendement à venir de l'ISO 1101 et l'ISO/FDIS 14405);

En France, la cotation GPS a été introduite au programme de l'enseignement technique ( avec les « fiches GPS » ^[4]) au milieu des années 1990, sous l'impulsion d'un inspecteur général, suite à un séminaire national de l'IGEN.

Démarche

On part d'une pièce dite « idéale ». L'idée générale est de comparer la pièce réelle, fabriquée, à la pièce idéale. Il faut donc pour cela procéder à des contrôles, soit par des moyens classiques — pied à coulisse, micromètre, marbre, cales et comparateur, piges, jauges, … —, soit avec une machine à mesurer tridimensionnelle (MMT ou « tridim' »).

Considérons une partie fonctionnelle de la pièce, par exemple un alésage (trou calibré). La cotation dimensionnelle va définir les variations admissibles du diamètre par rapport à la cote nominale, mais il peut aussi être nécessaire de préciser, par exemple,

• la perpendicularité par rapport à la surface ;
• le parallélisme de l'axe de l'alésage par rapport à un autre alésage ;
• la « régularité » du trou (cylindricité) ;
• …

Prenons l'exemple de la perpendicularité. Mathématiquement, on peut facilement déterminer l'angle que fait l'axe d'un cylindre par rapport à un plan. Mais ici, nous sommes en présence d'une surface réputée cylindrique — on dit encore nominalement cylindrique — et d'une surface réputée plane, mais qui présentent des irrégularités. Il faut donc, à partir de ces surfaces imparfaites, non-idéales, construire des surfaces parfaites, et les comparer.

Il existe plusieurs manières de faire, mais les normes en la matière s'attachent à permettre tant que faire se peut un contrôle par des moyens classiques.

Exemple : perpendicularité d'un alésage

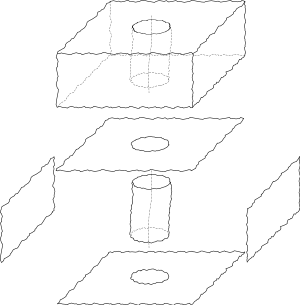
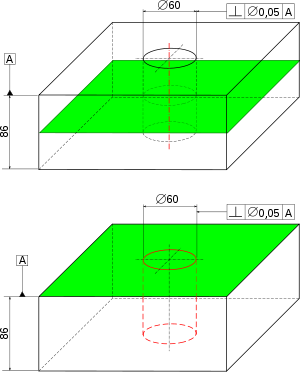
Développons l'exemple de la perpendicularité d'un alésage par rapport à une surface. La figure ci-contre montre

• une représentation en perspective de la pièce idéale avec la cotation de la perpendicularité ; A est le nom du plan, t est la tolérance (un nombre en millimètres, typiquement entre 0,01 et 1 mm) ;
• une représentation de la pièce réellement réalisée ; les défauts sont amplifiés (anamorphose).

Du modèle de peau à l'objet idéal

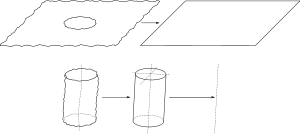
On considère la pièce réelle, et on en « extrait » la partie qui nous intéresse, ici l'alésage ; on dit que l'on partitionne la pièce. La surface de cette partie, surface non idéale, est appelée modèle de peau ou skin model. Puis, on détermine un objet idéal à partir de ce modèle de peau, ici, le cylindre parfait du plus grand diamètre inscrit dans l'alésage. D'un point de vue du contrôle, cela revient à essayer différentes piges — des cylindres calibrés — de diamètre croissant et à retenir la pige la plus grande entrant dans le trou, ou bien à utiliser un mandrin expansible.

Ce cylindre idéal est le cylindre associé à l'alésage ; il a un axe et une surface, on s'intéresse ici à son axe.

Puis, on isole la surface nominalement plane, et on prend le plan tangent ayant la direction moyenne du plan. D'un point de vue du contrôle, cela revient à poser la pièce sur un marbre ; d'un point de vue mathématique, on détermine le plan parfait minimisant l'écart quadratique par rapport à la surface réelle (méthode des moindres carrés, voir l'article Régression linéaire), et on le translate pour qu'il soit à l'extérieur de la matière. Ce plan idéal est le plan associé à la surface réelle.

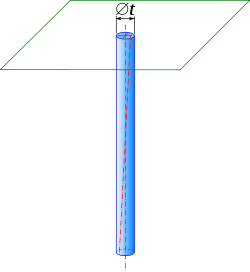
Repère et zone de tolérance

Reste à définir les orientations acceptables de l'axe par rapport au plan. Pour cela, on prend la normale au plan, et on construit un cylindre ayant pour axe cette normale, et ayant pour diamètre la tolérance, indiquée en millimètres ; c'est la zone de tolérance (ZT). L'alésage est conforme si l'axe du cylindre parfait associé peut être placé entièrement dans cette zone de tolérance.

La perpendicularité est une affaire d'angle, on pourrait donc pu s'attendre à ce que l'on définisse une tolérance en degrés, la zone de tolérance aurait alors été un cône. Mais en cotation GPS, les tolérances sont toujours indiquées en millimètre, les zones de tolérances sont toujours des formes extrudées (ayant une section droite uniforme), à quelques exceptions près (tolérances de forme quelconque).

Principes fondamentaux

Principe d'indépendance

Le premier principe du tolérancement géométrique est le principe d'indépendance :

les tolérances dimensionnelles et les tolérances géométriques sont indépendantes.

Cela signifie qu'une cote indique soit une tolérance dimensionnelle, soit une tolérance géométrique. De fait, les dimensions sont déterminées localement et non globalement : on considère la distance entre des points pris deux à deux, et non pas une enveloppe devant contenir la surface. On ne peut mettre en place une cote dimensionnelle que si l'on peut matériellement vérifier la distance entre paires de points ; par exemple, on ne peut pas tolérancer la distance d'un élément par rapport à l'axe d'un perçage puisque cet axe n'a pas de point matériel permettant la mesure.

Il existe quelques exceptions à ce principe d'indépendance (voir plus bas).

Vocabulaire et opérations de base

Le tolérancement s'intéresse à des objets géométriques, qui sont des points, des lignes et des surfaces. On distingue

• les objets non-idéaux, qui sont les objets extraits des produits réellement fabriqués ou du modèle de peau ; pour une cote donnée, on a deux types d'objets non-idéaux :
  • les éléments tolérancés, qui sont ceux que l'on veut caractériser, et
  • les éléments de référence, qui sont ceux par rapport auxquels on définit la tolérance ;
• les objets idéaux, qui sont des formes géométriquement parfaites : plan, cylindre, cône, …
  • l'objet idéal réprésentant un élément de référence est appelé « référence spécifiée ».

Les objets non-idéaux sont aussi appelés « modèle de peau » (skin model) : on ne s'intéresse pas à la matière, mais uniquement à la forme de la surface ou de la ligne, à la « peau » de l'objet.

Nom des objets géométriques

	Objet idéal	Objet non-idéal (modèle de peau)
servant de référence	référence spécifiée	référence, élément de référence
à caractériser		élément tolérancé

Le tolérancement géométrique nécessite de « créer » des objets idéaux ou non-idéaux, soit à partir du dessin de définition, soit à partir de la pièce réelle. On définit pour cela des « opérations », les principales sont :

• partition : cela consiste à considérer séparément chaque point, ligne ou surface concernée par la cotation ; ce sont les surfaces réelles, les modèles de peau ; cela permet d'identifier un élément tolérancé ou un élément de référence ;
• association : cela consiste à définir l'objet idéal à partir du modèle de peau, à ajuster le modèle idéal à la surface réelle ;
• construction : cela consiste à construire un objet idéal à partir d'un ou plusieurs objets idéaux, par exemple construire l'axe d'un cylindre idéal, construire la normale à un plan idéal, construire le plan de symétrie de deux plan idéaux, …
• évaluation : cela consiste à vérifier que le modèle de peau est dans la zone de tolérance.

On utilise en outre les opérations suivantes :

• extraction : c'est l'échantillonnage d'une surface, le fait d'extraire des points d'un modèle de peau ; cela correspond à la palpation par une machine à mesurer tridimensionnelle ;
• collection : réunion de plusieurs objets.

D'un point de vue du vocabulaire, il faut donc bien distinguer la « référence », qui est un élément non-idéal, de la « référence spécifiée », qui est un objet idéal associé à une référence.

Références

Les tolérances de forme ne font appel à aucune référence. Par contre, pour les autres tolérances géométriques, il faut utiliser une ou plusieurs références. Lorsqu'il y en a plusieurs, on parle de « système de référence » et l'ordre a de l'importance ; la première citée est la « référence primaire », la seconde la « référence secondaire » et ainsi de suite. On peut avoir jusqu'à six références, mais la plupart du temps on en a une à trois.

L'ordre des références présente des similitudes avec l'isostatisme dans la mise en position des pièces (MiP). Lors de la cotation du dessin, le concepteur doit avoir en tête la manière dont la pièce va être fabriquée et contrôlée, afin justement que les références correspondent aux surfaces et arrêtes utilisées pour la mise en position.

Référence primaire

La référence primaire, éventuellement référence unique, est une surface plane ou un cylindre :

• surface plane : c'est l'équivalent de l'appui plan (on bloque une translation et deux rotations), cela permet de définir un axe normal au plan ;
• cylindre : c'est l'équivalent d'un centrage long (on bloque deux translations et deux rotations), cela permet de définir un axe qui est l'axe du cylindre.

L'axe en question est le premier axe du repère.

Référence secondaire

On peut avoir besoin d'une référence secondaire. Si la référence primaire est un plan, alors

• si la référence secondaire est un plan, ce plan est perpendiculaire au plan de référence primaire et est tangent à la pièce du côté extérieur à la matière ; on considère la droite normale à ce plan, cette droite forme le second axe du repère ; cette situation est similaire à un appui linéaire dans la MiP (orientation de la pièce) ;
• si la référence secondaire est un cylindre, on ne considère que son intersection avec la plan de référence primaire ; le centre de ce cercle forme l'origine du repère ; cette situation est similaire à un centrage court dans la MiP.

Référence tertiaire

On peut avoir besoin d'une référence tertiaire. Si trois références sont des plans, alors la référence tertiaire agit comme un appui ponctuel : il ne définit pas de direction, mais uniquement une origine.

Zone commune, référence commune

Exécution graphique de la cotation

L'indication de la cote sur le dessin de définition suit un formalisme rigoureux.

Les références sont indiquées par une lettre encadrée, reliée à la l'élément de référence par un trait fin s'attachant à l'élément par un triangle noir plein. On distingue deux cas :

• l'étiquette est alignée sur la flèche de cote dimensionnelle : on considère alors l'élément médian : axe pour un cylindre, plan de symétrie pour deux faces parallèles ;
• l'étiquette est décalée par rapport à la flèche de cote dimensionnelle : on considère alors l'élément pointé en lui-même.

De la même manière, si la flèche de cote géométrique est alignée avec la flèche de cote dimensionnelle, l'élément tolérancé est l'élément médian ; si la flèche de cote géométrique n'est pas alignée, c'est l'élément désigné qui est tolérancé.

La cotation d'un élément est composée de plusieurs cadres successif comprenant :

• le symbole représentant le type de tolérance (perpendicularité, localisation, coaxialité, …) ;
• la tolérance, exprimée en millimètre (typiquement entre 0,01 et 1 mm) ; si la tolérance est un diamètre (précédée du symbole ∅), la zone est cylindrique, sinon elle est parallélépipédique (sauf tolérance de forme quelconque) ;
• le cas échéant, une ou plusieurs références.

Un même élément peut comporter plusieurs cotes GPS, par exemple une cote de localisation et d'orientation ; les cotes sont alors indiquées l'une en dessous de l'autre.

Le trait de cotation pointe sur l'élément tolérancé ou sur une ligne d'attache d'une cote dimensionnelle de cet élément.

Les cotes dimensionnelles jouant un rôle dans la cotation GPS d'un élément sont encadrées.

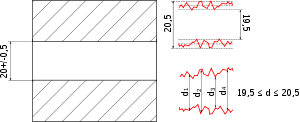
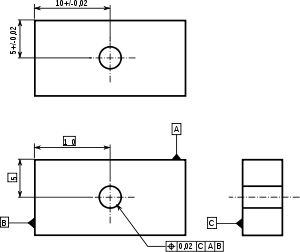
Concernant l'exemple ci-contre, pour la cotation GPS (image du bas) :

• les plans de référence sont indiqués par les étiquettes A, B et C ;
• le plan C est le plan principal pour le système de référence ; tout est construit perpendiculairement à lui, et en particulier l'axe de la zone de tolérance ; la référence secondaire est le plan A, la référence tertiaire le plan B ;
• les cotes encadrées vont permettre de placer la zone de tolérance par rapport aux plans de référence ;
• la cote GPS indique que :
  • il s'agit d'une tolérance de localisation : symbole ⊕,
  • la zone de tolérance est un carré de 0,02 mm de côté ;
  • le carré est positionné par rapport à A et B selon les cotes encadrées.

La notation GPS est prend plus de place que la cotation « traditionnelle », mais elle lève toutes les ambiguïtés.

Les différentes tolérances

Tolérances de forme

Les tolérances de forme ne font appel à aucun repère ; les zones de tolérance ne sont ni contrainte en position, ni en orientation (principe d'indépendance) .

Il faut distinguer les tolérances de forme de la rugosité, voir l'article État de surface.

Ligne quelconque

Le cas général de la forme d'une ligne quelconque.

Surface quelconque

Le cas général de la forme d'une surface quelconque.

Rectitude

Le cas particulier de la rectitude.

Une ligne quelconque du plan suivant une direction donnée, doit être comprise entre deux droites parallèles distante de la valeur de la tolérance.

Circularité

Le cas particulier de la circularité.

Le profil (que l'on espère assez proche de la forme circulaire !) doit être compris entre deux cercles concentriques et coplanaires dont la différence des rayons est inférieure ou égale à la valeur de tolérance. La circonférence intérieure est la plus grande circonférence inscrite dans le profil tandis que la circonférence extérieure est la plus petite circonférence circonscrite dans le profil.

Planéité

Le cas particulier de la planéité.

On parlera de « surface plane », un « plan » étant un objet s'étendant à l'infini. Pour une surface réelle, on parle de « surface réputée plane » ou de « surface nominalement plane ».

La surface plane tolérancée doit être comprise entre deux plans parallèles distants de la valeur de la tolérance donnée.

Cylindricité

Le cas particulier de la cylindricité.

La surface tolerancée doit être comprise entre deux cylindres coaxiaux dont les rayons diffèrent de la valeur de la tolérance. Le cylindre extérieur est le plus petit cylindre circonscrit.

Tolérances d'orientation

Ligne quelconque

Le cas général de la forme d'une ligne quelconque.

Surface quelconque

Le cas général de la forme d'une surface quelconque.

Inclinaison

Le cas général de l'inclinaison.

La surface tolérancée est comprise dans une zone de tolérance définie par deux plans parallèles distants de la valeur de la tolérance. La zone de tolérance est contrainte en orientation seulement.

Parallélisme

Le cas particulier du parallélisme.

La surface tolérancée est comprise dans une zone de tolérance définie par deux plans parallèles distants de la valeur de la tolérance et parallèles au plan de référence. la zone de tolérance est contrainte en orientation seulement.

Perpendicularité

Le cas particulier de la perpendicularité.

Tolérances de position

Ligne quelconque

Le cas général de la forme d'une ligne quelconque.

Surface quelconque

Le cas général de la forme d'une surface quelconque.

Spécification de localisation

Le cas général de la localisation.

Coaxialité/concentricité

Le cas particulier de la coaxialité/concentricité.

Symétrie

Le cas particulier de la symétrie.

Tolérances de battement

Battement simple

Le cas général du battement simple.

Battement simple axial

La zone de tolérance est limitée pour chaque position radiale, par deux circonférences distantes de t situées sur le cylindre de mesurage dont l'axe coïncide avec l'axe de référence.

Battement simple radial

La zone de tolérance est limitée dans chaque plan de mesurage perpendiculaire à l'axe par deux cercles concentriques distants de t dont le centre coïncide avec l'axe de référence.

Battement simple oblique

La zone de tolérance est limitée sur chaque cone de mesurage par deux circonférences distantes de t. Chaque cone de mesurage a ses génératrices dans la direction spécifiée et son axe coïncide avec l'axe de référence.

Battement total

Le cas général du battement total.

Exceptions au principe d'indépendance

Exigence de l'enveloppe

L'exigence d'enveloppe consiste à imposer que l'objet tolérancé soit compris dans une enveloppe parfaite au maximum de la tolérance dimensionnelle. Elle s'indique par un E entouré Ⓔ placé après la valeur de la cote dimensionnelle.

Exigence du maximum de matière

L'exigence du maximum de matière revient à considérer la montabilité d'un système. L'idée est qu'un défaut peut compenser un autre défaut, ce qui permet d'accepter des pièces qui, si l'on considérait les défaut indépendamment, auraient été rebutées.

Considérons par exemple un système pièce mâle/pièce femelle, la pièce mâle comparant deux protubérances cylindriques et la pièce femelle deux alésages. Pour que le système soit montable, il faut pour chaque pièce

• que les cylindres aient un diamètre correct ;
• que la distance séparant les diamètres soit correcte.

On a donc une tolérance de localisation d'un cylindre par rapport à l'autre, et une tolérance dimensionnelle sur le diamètre.

Mais si un cylindre est plus petit, il y a plus de jeu, ce qui permet d'avoir une erreur plus grande sur la localisation. Mais alors la cote géométrique n'est plus indépendante de la cote dimensionnelle.

On travaille alors avec une zone de tolérance unique qui concerne le cylindre en entier : tant que le cylindre est compris en entier dans la ZT, peu importe son diamètre exact ou sa localisation exacte. Cette ZT est obtenue en considérant le maximum de matière, c'est-à-dire la protubérance de plus grand diamètre ou l'alésage de plus petit diamètre.

L'exigence du maximum de matière s'indique par un M entouré Ⓜ placé après la cote dimensionnelle.

Exigence du minimum de matière

L'exigence du minimum de matière est indiquée par un L entouré Ⓛ placé après la cote dimensionnelle.

Notes

Voir aussi

• Cotation fonctionnelle
• Cotation de fabrication

• Portail de la physique