Théorème de herbrand-ribet

Théorème de Herbrand-Ribet

Le théorème de Herbrand-Ribet est un renforcement du théorème de Kummer avec pour effet le fait que le nombre premier p divise le nombre de classes du corps cyclotomique des racines p-ièmes de l'unité si et seulement si p divise le dénominateur du n-ième nombre de Bernoulli 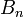$B_n\,$ pour un certain n, 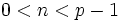$0 < n < p - 1\,$ . Le théorème de Herbrand-Ribet précise ce que veut dire, en particulier, lorsque p divise $B_n\,$ .

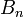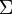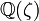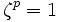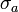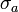Le groupe de Galois $\Sigma\,$ du corps cyclotomique des racines p-ièmes de l'unité pour un nombre premier impair p, $\mathbb{Q}(\zeta)$ avec $\zeta^p = 1\,$ , est constitué des p - 1 éléments $\sigma_a\,$ , où $\sigma_a\,$ est défini par le fait que 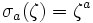$\sigma_a(\zeta) = \zeta^a\,$ . Comme conséquence du petit théorème de Fermat, dans l'anneau des entiers p-adiques 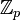$\mathbb{Z}_p$ , nous avons p - 1 racines de l'unité, chacune d'elles est congrue mod p à un certain nombre dans l'intervalle 1 à p - 1; nous pouvons par conséquent définir un caractère de Dirichlet 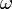$\omega\,$ (le caractère de Teichmüller) avec des valeurs dans 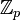$\mathbb{Z}_p$ en requérant ceci pour n relativement premier à p, 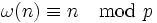$\omega(n) \equiv n \mod{p}\,$ . La partie p du groupe de classes est un 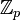$\mathbb{Z}_p$ -module, et nous pouvons appliquer les éléments dans l'anneau $\mathbb{Z}_p[\Sigma]$ vers lui et obtenir les éléments du groupe de classes. Nous pouvons maintenant définir un élément idempotent de l'anneau pour chaque n de 1 à p - 1, comme

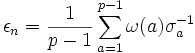$\epsilon_n = \frac{1}{p-1}\sum_{a=1}^{p-1} \omega(a) \sigma_a^{-1}\,$ .

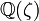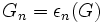Nous pouvons maintenant séparer la partie p du groupe des classes d'idéaux G de $\mathbb{Q}(\zeta)$ par identification des idempotents; si G est le groupe des classes d'idéaux, alors $G_n = \epsilon_n(G)\,$ .

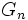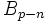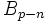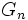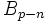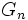Alors, nous avons le théorème de Herbrand-Ribet : $G_n\,$ ne contient pas d'élément si et seulement si p divise le nombre de Bernoulli $B_{p - n}\,$ . La partie exprimant p divise $B_{p - n}\,$ si $G_n\,$ est non trivial est due à Herbrand. La réciproque, si p divise $B_{p - n}\,$ alors $G_n\,$ est non trivial est due à Ribet, et est considérablement plus difficile. Par la théorie des corps de classes, ceci peut être vrai s'il existe une extension non-ramifiée du corps des racines p-ièmes de l'unité par une extension cyclique de degré p qui se comporte d'une manière précise sous l'action de 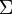$\Sigma\,$ ; Ribet démontra ceci par une construction concrète d'une telle extension.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Herbrand-Ribet ».

Catégories : Corps cyclotomiques | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de herbrand-ribet de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Theoreme de Herbrand-Ribet — Théorème de Herbrand Ribet Le théorème de Herbrand Ribet est un renforcement du théorème de Kummer avec pour effet le fait que le nombre premier p divise le nombre de classes du corps cyclotomique des racines p ièmes de l unité si et seulement si … Wikipédia en Français
Théorème de Herbrand-Ribet — Le théorème de Herbrand Ribet est un renforcement du théorème de Kummer avec pour effet le fait que le nombre premier p divise le nombre de classes du corps cyclotomique des racines p ièmes de l unité si et seulement si p divise le numérateur du… … Wikipédia en Français
Théorème de Stickelberger — En mathématiques, le théorème de Stickelberger est un résultat de la théorie algébrique des nombres, qui donne certaines informations sur la structure du module de Galois des groupes de classes des corps cyclotomiques. Il est a été démontré par… … Wikipédia en Français
Jacques Herbrand — Pour les articles homonymes, voir Herbrand. Dernière photographie de Jacques Herbrand prise au cours de l excursion où il trouva la mort Jacques Herbrand, né à Paris le 12 février … Wikipédia en Français
Kenneth Alan Ribet — Ken Ribet Ken Ribet en 2007 au CIRM Naissance 28 juin 1948 (États Unis) Domicile États Unis Nationalité … Wikipédia en Français
Demonstrations du petit theoreme de Fermat — Petit théorème de Fermat Pierre de Fermat propose le théorème sans apporter de démonstration. En mathématiques, le petit théorème de Fermat est un résultat de l arithmétique modulaire, qui peut aussi se démontrer avec les outils de l arithmétique … Wikipédia en Français
Démonstrations Du Petit Théorème De Fermat — Petit théorème de Fermat Pierre de Fermat propose le théorème sans apporter de démonstration. En mathématiques, le petit théorème de Fermat est un résultat de l arithmétique modulaire, qui peut aussi se démontrer avec les outils de l arithmétique … Wikipédia en Français
Démonstrations du petit théorème de Fermat — Petit théorème de Fermat Pierre de Fermat propose le théorème sans apporter de démonstration. En mathématiques, le petit théorème de Fermat est un résultat de l arithmétique modulaire, qui peut aussi se démontrer avec les outils de l arithmétique … Wikipédia en Français
Démonstrations du petit théorème de fermat — Petit théorème de Fermat Pierre de Fermat propose le théorème sans apporter de démonstration. En mathématiques, le petit théorème de Fermat est un résultat de l arithmétique modulaire, qui peut aussi se démontrer avec les outils de l arithmétique … Wikipédia en Français
Petit theoreme de Fermat — Petit théorème de Fermat Pierre de Fermat propose le théorème sans apporter de démonstration. En mathématiques, le petit théorème de Fermat est un résultat de l arithmétique modulaire, qui peut aussi se démontrer avec les outils de l arithmétique … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de herbrand-ribet