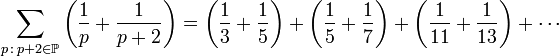Théorème de brun

Théorème de Brun

Le théorème de Brun énonce le fait que la série des inverses des nombres premiers jumeaux est convergente. Sa limite est appelée constante de Brun.

Autrelent dit la somme :

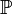$\sum\limits_{ p \, : \, p + 2 \in \mathbb{P} } {\left( {\frac{1}{p} + \frac{1}{{p + 2}}} \right)} = \left( {\frac{1}{3} + \frac{1}{5}} \right) + \left( {\frac{1}{5} + \frac{1}{7}} \right) + \left( {\frac{1}{{11}} + \frac{1}{{13}}} \right) + \cdots$

(où $\mathbb{P}$ désigne l'ensemble des nombres premiers) est finie.

Note historique

Le mathématicien norvégien Viggo Brun restera dans les mémoires comme étant l'inventeur des méthodes modernes de cribles combinatoires. Entre 1917 et 1924, il inventera et perfectionnera cette théorie, dont le principe repose sur le crible d'Eratosthène. L'utilisation du principe d'inclusion-exclusion (appelé aussi en combinatoire inégalités de Bonferroni) permet de théoriser ce crible : si l'on pose (pour $x$ assez grand)

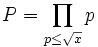$P = \prod_{p \leq \sqrt x} p$ le produit des nombres premiers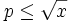 $p \leq \sqrt x$

alors une condition nécessaire et suffisante pour qu'un entier $n$ tel que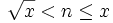 $\sqrt x < n \leq x$ soit premier est que $p g c d (n, P) = 1$ .

Ainsi, si $π(x)$ désigne le nombre de nombres premiers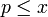 $p \leq x$ et si l'on pose $e 1$ la fonction arithmétique valant 1 si $n = 1$ et 0 sinon, alors le crible d'Eratosthène s'écrit :

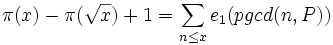$\pi(x) - \pi(\sqrt{x}) + 1 = \sum_{n \leq x} e_1(pgcd(n,P))$ .

En utilisant la formule d'inversion de Möbius, il vient :

$\pi(x) - \pi(\sqrt{x}) + 1 = \sum_{d \mid P} \mu(d) \left [ \frac {x}{d} \right ]$ ,

où $[t]$ désigne la partie entière du réel t.

Comment estimer cette dernière somme ? A ce stade, si l'on utilise l'égalité évidente $[t] = t + O (1)$ , on obtient un terme d'erreur de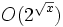 $O(2^{\sqrt {x}})$ bien trop gros pour fournir des renseignements quant à la distribution des nombres premiers.

En fait, ce crible d'Eratosthène repose sur la formule d'inversion de Möbius qui s'écrit plus simplement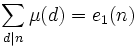 $\sum_{d \mid n} \mu(d) = e_1(n)$ , formule trop "directe" pour être utilisable en pratique.

L'idée de Brun consiste à déterminer deux fonctions, notées disons $μ 1$ et $μ 2$ , de sorte que l'on ait

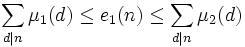
$\sum_{d \mid n} \mu_1(d) \leq e_1(n) \leq \sum_{d \mid n} \mu_2(d)$

et telles que ces fonctions s'annulent suffisamment souvent pour obtenir des termes d'erreurs exploitables.

La détermination de telles fonctions pose un problème délicat d'optimisation, et ce travail est toujours d'actualité aujourd'hui.

Brun a choisi les fonctions suivantes :

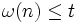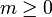Si l'on note $1 t$ la fonction indicatrice de l'ensemble des entiers $n$ tels que $\omega(n) \leq t$ (où $ω(n)$ désigne le nombre de facteurs premiers distincts de $n$ ), alors on peut prendre pour tout entier $m \geq 0$ :

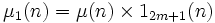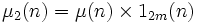$\mu_1(n) = \mu(n) \times 1_{2m+1}(n)$ et $\mu_2(n) = \mu(n) \times 1_{2m}(n)$ .

La théorie reposant sur ces fonctions conduit alors au résultat essentiel suivant :

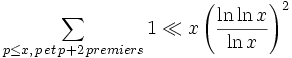$\sum_{p \leq x, \, p \, et \, p+2 \, premiers} 1 \ll x \left ( \frac {\ln \ln x}{\ln x} \right )^2$ ,

d'où l'on déduit que la série des inverses des nombres premiers jumeaux converge.

Liens externes

Le numéro du Bulletin des sciences mathématiques (1919, pages 100 et suivantes) dans lequel Brun énonce et démontre le théorème.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Brun ».

Catégorie : Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de brun de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Théorème de Brun — Le théorème de Brun énonce le fait que la série des inverses des nombres premiers jumeaux est convergente. Sa limite est appelée constante de Brun. Autrement dit la somme : (où désigne l ensemble des nombres premiers) est finie … Wikipédia en Français
Brun — (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Brun (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Brun (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Brun (homonymie) », sur le Wiktionnaire (dictionnaire universel) … Wikipédia en Français
Jean brun (homonymie) — Brun (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Viggo Brun — est un mathématicien norvégien né en le 13 octobre 1882 à Lier et mort le 15 août 1978 à Drøbak. Il est essentiellement connu pour son théorème montrant que la somme des inverses des nombres premiers jumeaux est convergente. En son honneur on a… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Histoire De La Fonction Zeta De Riemann — Histoire de la fonction zêta de Riemann Cet article présente une histoire de la fonction zêta de Riemann. Pour une présentation mathématique de la fonction et de ses propriétés, voir : Article principal : fonction zêta de Riemann. Un… … Wikipédia en Français
Histoire de la fonction Zeta de Riemann — Histoire de la fonction zêta de Riemann Cet article présente une histoire de la fonction zêta de Riemann. Pour une présentation mathématique de la fonction et de ses propriétés, voir : Article principal : fonction zêta de Riemann. Un… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de brun