Théorème de Péano

Théorème de Péano

Théorème de Cauchy-Peano-Arzelà

Page d'aide sur l'homonymie Pour les articles homonymes, voir Cauchy.

Enoncé

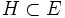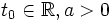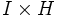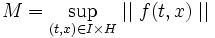Soient E un Espace de Banach de dimension finie, H \subset E une partie ouverte convexe de E. Soit I = [t0 − a,t0 + a] un intervalle de \mathbb{R} (t_0\in \mathbb{R},a>0), soit f une fonction continue et bornée de I\times H dans E. Soit M= \sup_{(t,x)\in I\times H} \mid \mid f(t,x)\mid \mid.
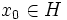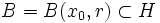Soient x_0\in H et r > 0 tels que B=B(x_0,r) \subset H.
Alors, il existe une solution au problème :
x' = f(t,x)
x(t0) = x0
définie sur l'intervalle [t0 − c,t0 + c] où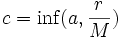 c=\inf(a,\frac{r}{M}), et à valeurs dans B.

N.B. : Contrairement à ce que permet de conclure le théorème de Cauchy-Lipschitz sous des hypothèses plus restrictives, il n'y a pas unicité ici.

Exemples

Les exemples suivants donnés par Peano[1]

L'équation 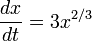\frac{dx}{dt}=3x^{2/3} où le second membre est continu en x=0 sans être lipschitzien, admet les solutions x = t3 et x = 0 qui s'annulent toutes les deux en t = 0 ainsi que les fonctions qui sont nulles dans l'intervalle [0,a] et qui prennent la valeur (t − a)3 pour t > a.

L'équation 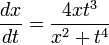\frac{dx}{dt}=\frac{4xt^3}{x^2+t^4} toujours avec la condition x(0)=0, admet les cinq solutions (C étant une constante arbitraire positive)

  1. x(t) = t2
  2. x(t) = − t2
  3. x(t) = 0
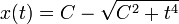
  4. x(t)=C-\sqrt{C^2+t^4}
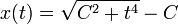
  5. x(t)=\sqrt{C^2+t^4}-C

Références

  1. ↑ Peano,Démonstration de l'intégrabilité des équations différentielles ordinaires,Mathematische annalen, T37,1890,p227
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Cauchy-Peano-Arzel%C3%A0 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Péano de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Théorème de Peano — Théorème de Cauchy Peano Arzelà Pour les articles homonymes, voir Cauchy. Enoncé Soient E un Espace de Banach de dimension finie, une partie ouverte convexe de E. Soit I = [t0 − a,t0 + a] un intervalle de …   Wikipédia en Français

  • Theoreme de Jordan — Théorème de Jordan La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de… …   Wikipédia en Français

  • Théorème de Jordan-Brouwer — Théorème de Jordan La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de… …   Wikipédia en Français

  • Théorème de jordan — La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de Jordan est un… …   Wikipédia en Français

  • Théorème de Jordan — En mathématiques, le théorème de Jordan est un théorème de topologie plane. Il est célèbre par le caractère apparemment intuitif de son énoncé et la difficulté de sa démonstration. « En fait, il n y a pratiquement aucun autre théorème qui… …   Wikipédia en Français

  • Peano — Giuseppe Peano Giuseppe Peano Giuseppe Peano (Spinetta di Cuneo (Coni), 27 août 1858 Turin, 20 avril 1932) est un mathématicien italien de la fin du XIXe et du début du …   Wikipédia en Français

  • Theoreme d'incompletude de Godel — Théorème d incomplétude de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und… …   Wikipédia en Français

  • Théorème d'incomplétude — de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (Sur les… …   Wikipédia en Français

  • Théorème d'incomplétude de Godel — Théorème d incomplétude de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und… …   Wikipédia en Français

  • Théorème d'incomplétude de Gödel — Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (Sur les propositions …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”