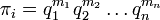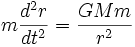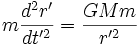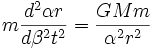Théorème de Buckingham

En mathématiques, le théorème de Vaschy-Buckingham, ou théorème Pi, est un des théorèmes de base de l'analyse dimensionnelle.

Sommaire

1 Énoncé
2 Démonstration de la 3^e loi de Kepler
3 Références
4 Voir aussi

Énoncé

Une équation physique complète, de la forme générale…

$f(q_1, q_2, \cdots, q_n)= 0$

où les $q i$ représentent $n$ variables physiques choisies pour la description du problème, exprimées en termes de $k$ unités physiques indépendantes, peut être réécrite sous la forme:

$F(\pi_1,\pi_2,\ldots,\pi_p)=0$

où les $π i$ sont des nombres sans dimension construits à partir des $q i$ par $p = n - k$ équations de la forme:

$\pi_i=q_1^{m_1}q_2^{m_2}\ldots q_n^{m_n}$

où les $m i$ sont des constantes.

Démonstration de la 3^e loi de Kepler

Le théorème de Buckingham suppose grossièrement que toutes les lois de la physique restent valables quelle que soit l'échelle utilisée, c'est-à-dire en particulier même après un étirement des longueurs et du temps.

Supposons donc que l'on étire les longueurs (notées $r$ ) de $α$ et le temps (noté $t$ ) de $β$ . On pose alors

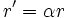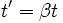$r'=\alpha r\,$ et $t'=\beta t\,$ .

Soient une particule fixe de masse $M$ et une particule mobile de masse $m$ $(m < < M)$ soumise uniquement à la force gravitationnelle de la particule de masse $M$ . En écrivant le principe fondamental de la dynamique selon un axe reliant le centre des deux particules, on a:

$m\frac{d^2r}{dt^2} = \frac{GMm}{r^2}\,$

D'après le théorème de Buckingham, on devrait avoir également

$m\frac{d^2r'}{dt'^2} = \frac{GMm}{r'^2}\,$

Soit en remplaçant:

$m\frac{d^2\alpha r}{d\beta^2 t^2} = \frac{GMm}{\alpha^2 r^2}\,$

Soit nécessairement :

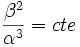
$\frac{\beta^2}{\alpha^3}=cte\,$

pour obtenir l'équation initiale.

On retrouve alors bien la troisième loi de Kepler ( $β$ étant associé au temps et $α$ aux longueurs).

Références

Buckingham, E. (1914) Phys. Rev. 4, 345-376. Et une généralisation de ce théorème dans le cas de classes de problèmes où certaines variables sont fixes : [1]

Voir aussi

Portail de la physique
Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Buckingham ».

Catégories : Théorème d'analyse | Métrologie | Théorème de physique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Buckingham de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Theoreme de Buckingham — Théorème de Buckingham En mathématiques, le théorème de Vaschy Buckingham, ou théorème Pi, est un des théorèmes de base de l analyse dimensionnelle. Sommaire 1 Énoncé 2 Démonstration de la 3e loi de Kepler 3 Références … Wikipédia en Français
Théorème Vaschy-Buckingham — Théorème de Buckingham En mathématiques, le théorème de Vaschy Buckingham, ou théorème Pi, est un des théorèmes de base de l analyse dimensionnelle. Sommaire 1 Énoncé 2 Démonstration de la 3e loi de Kepler 3 Références … Wikipédia en Français
Théorème de buckingham — En mathématiques, le théorème de Vaschy Buckingham, ou théorème Pi, est un des théorèmes de base de l analyse dimensionnelle. Sommaire 1 Énoncé 2 Démonstration de la 3e loi de Kepler 3 Références … Wikipédia en Français
Théorème PI — Théorème de Buckingham En mathématiques, le théorème de Vaschy Buckingham, ou théorème Pi, est un des théorèmes de base de l analyse dimensionnelle. Sommaire 1 Énoncé 2 Démonstration de la 3e loi de Kepler 3 Références … Wikipédia en Français
Théorème Pi — Théorème de Buckingham En mathématiques, le théorème de Vaschy Buckingham, ou théorème Pi, est un des théorèmes de base de l analyse dimensionnelle. Sommaire 1 Énoncé 2 Démonstration de la 3e loi de Kepler 3 Références … Wikipédia en Français
Théorème pi — Théorème de Buckingham En mathématiques, le théorème de Vaschy Buckingham, ou théorème Pi, est un des théorèmes de base de l analyse dimensionnelle. Sommaire 1 Énoncé 2 Démonstration de la 3e loi de Kepler 3 Références … Wikipédia en Français
Théorème de Vaschy-Buckingham — En mathématiques, le théorème de Vaschy Buckingham[1],[2], ou théorème Pi, est un des théorèmes de base de l analyse dimensionnelle. Ce théorème établit que si une équation physique met en jeu n variables physiques, celles ci dépendant de k… … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de Buckingham