Théorie de la percolation

Le modèle mathématique de la percolation a été introduit par John Hammersley en 1957. Il s'intéresse aux caractéristiques des milieux aléatoires, plus précisément aux ensembles de sommets connectés dans un graphe aléatoire.

Informellement, imaginons que l'on place de l'eau au sommet d'une pierre spongieuse. S'il y a assez de petits canaux, il est alors possible qu'il y ait un chemin du centre de la pierre vers l'extérieur. Ce modèle permet de répondre à ce genre de question.

Différents types de percolation

Cette théorie s'applique à la science des matériaux, dans le domaine de la percolation.

Description du modèle de base

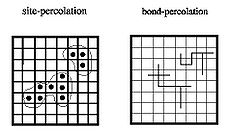
Soit p un paramètre compris entre 0 et 1. Deux points (ou sommets) à distance euclidienne 1 du réseau d-dimensionnel Z^d (deux tels points sont dits voisins) sont alors reliés avec probabilité p par une arête. Le résultat est un graphe aléatoire infini.

La probabilité de percolation de ce graphe, notée θ(p) est la probabilité que ce graphe admette une composante connexe (aussi appelée amas) de taille infinie.

Par des arguments de couplage, on montre que θ est une fonction croissante de p. On montre également qu'il existe un point critique p_c tel que θ(p) est nulle si p < p_c et strictement positive si p > p_c. Harry Kesten a montré qu'en dimension 2, p_c = 1 / 2.

Le régime sous-critique p < p_c

Dans ce régime, il n'y a pas de chemin infini dans le graphe. Les composantes connexes (appelé aussi amas) finies sont généralement de petite taille. Plus précisément la probabilité que l'amas contenant le point x ait une taille qui dépasse n décroît exponentiellement vite avec n. En particulier, la taille moyenne d'un amas est finie.

Le régime critique p = p_c

Ce régime est encore mal connu (à l'exception notable de la dimension 2). On conjecture que θ(p_c) = 0, c’est-à-dire qu'il n'y a pas de percolation au point critique, mais ceci n'est pour l'instant démontré qu'en dimension deux ou en grande dimension d > 18. En particulier, le cas de la dimension trois, dont la pertinence physique est évidente, demeure non prouvé.

Le régime sur-critique p > p_c

Dans la phase surcritique, il y a une unique composante infinie de points connectés. Cependant, les amas finis sont généralement de petite taille. L'amas infini rencontre tout l'espace; plus précisément la proportion de points d'une boîte de taille n qui appartiennent à l'amas infini tend vers θ(p_c) > 0 lorsque n tend vers l'infini. On sait aussi que l'amas infini est très rugueux : la proportion des points d'une boîte de taille n qui sont à la frontière de l'amas infini parmi la totalité des points de l'amas infini qui sont dans cette boîte tend vers 1 − p lorsque n tend vers l'infini.

Modèle continu

La théorie de la percolation s'étend aux milieux continus, comme par exemple les schémas booléens de sphères. Si les seuils de percolation sont différents de ceux observés dans les réseaux, les exposants critiques appartiennent à la même classe d'universalité que dans les réseaux.

Autres modèles

• La percolation orientée qui a des liens avec le processus de contact
• La percolation FK qui permet de relier la percolation au modèle d'Ising et au modèle de Potts.
• La percolation de premier passage

En physique

D'une manière générale, les exposants critiques observés pour les champs (expérimentalement ou à l'aide de modèle, par exemple dans les problèmes de conductivité, de mécanique, de permittivité) sont différents des exposants géométriques. Ces phénomènes traduisent l'effet de corrélations des champs dû aux intéractions physiques (ou du point de vue mathématique, aux équations différentielles associées). En particulier, les exposants sont distincts dans les réseaux et dans les milieux continus, de par l'existence de distances infiniment faibles entre interfaces, qui ne peuvent être limités par la taille des liens^[1].

On distingue en général deux types de percolation de premier et second ordre. Le premier cas regroupe les transitions de champs continues et se rencontrent en particulier dans les cas où le potentiel d'énergie possèdent un unique minimum. Au contraire, lorsque plusieurs minimaux locaux se développent, une transition discontinue peut apparaître. Ces phénomènes ne peuvent avoir lieu en théorie de la percolation standard.

Livres de références

• Percolation de G.R. Grimmett chez Springer
• Percolation Theory for Mathematicians de Harry Kesten chez Birkhaüser
• Stauffer et Aharony, Introduction to Percolation Theory, Taylor and Francis Ed. London, 1985

Notes et références

• Portail des probabilités et des statistiques