- Théorie de l'approximation/démonstrations
-
Théorie de l'approximation/Démonstrations
<< Retour à l'article Théorie de l'approximation
Un polynôme de degré n qui fournit une fonction d'erreur ayant n + 2 extrema de même grandeur en valeur absolue, les atteignant avec un changement de signe, est optimal.
Démonstration
Commençons par le montrer sur un graphique. Posons n = 4. Supposons que P soit un polynôme de degré n possédant les propriétés ci-dessus, dans le sens que P − f oscille entre n + 2 extrema de signes alternés, de
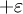à 
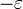.La fonction erreur P − f pourrait ressembler au graphique rouge:
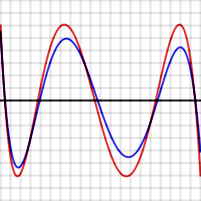L'erreur P − f pour le polynôme de niveau est représentée en rouge, et l'erreur pour le prétendu meilleur polynôme est représentée en bleu
P − f atteint n + 2 extrema (dont deux se trouvent aux extrémités), qui ont la même grandeur en valeur absolue situés dans 6 intervalles sur le graphique ci-dessus.
Supposons maintenant que Q, un autre polynôme de degré n, soit une strictement meilleure approximation que P. Cela signifie que les extrema de sa fonction erreur doivent tous avoir en valeur absolue une valeur strictement plus petite que
, de sorte qu'ils sont localisés strictement à l'intérieur du graphique d'erreur pour P. La fonction erreur pour Q pourrait avoir une représentation graphique ressemblant au graphique bleu ci-dessus. Cela signifie que (P − f) − (Q − f) doit osciller entre des nombres non nuls strictement positifs et strictement négatifs, un nombre total de n + 2 fois. Mais (P − f) − (Q − f) est égale à P − Q qui est un polynôme de degré n. Il doit avoir au moins les n + 1 racines situées entre différents points en lesquels la fonction polynôme prend des valeurs non nulles. D'après une conséquence du théorème de D'Alembert, c'est impossible.
Portail des mathématiques
Catégories : Polynôme | Théorie
Wikimedia Foundation. 2010.
