Theoreme de Mertens
- Theoreme de Mertens
-
Théorème de Mertens
On désigne habituellement sous le nom de premier théorème de Mertens l'estimation suivante, où, par convention, une somme (ou un produit) indexée par p désigne une somme (ou un produit) ne portant que sur les nombres premiers. Pour tout réel 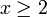 , on a :
, on a :
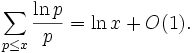
La démonstration utilise la formule de Legendre sur les valuations p-adiques de n!.
Le Second théorème de Mertens, appelé aussi formule de Mertens, stipule que, pour tout réel 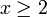 , on a :
, on a :
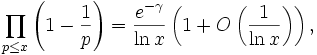
où 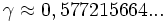 est la constante d'Euler-Mascheroni.
est la constante d'Euler-Mascheroni.
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorème de mathématiques | Analyse réelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Mertens de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de mertens — On désigne habituellement sous le nom de premier théorème de Mertens l estimation suivante, où, par convention, une somme (ou un produit) indexée par p désigne une somme (ou un produit) ne portant que sur les nombres premiers. Pour tout réel , on … Wikipédia en Français
Théorème de Mertens — En théorie des nombres, trois théorèmes de Mertens, démontrés en 1874 par Franz Mertens[1], sont reliés à la densité des nombres premiers. Un autre théorème de Mertens, en analyse, porte sur le produit de Cauchy de deux séries. Dans ce qui suit,… … Wikipédia en Français
Mertens — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Le nom de Mertens est porté par plusieurs personnalités (par ordre alphabétique) : Franz Mertens (1840 1927), mathématicien allemand. Franz … Wikipédia en Français
Constante de Meissel-Mertens — En mathématiques, la constante de Meissel (de) Mertens (également nommée constante de Mertens, constante de Kronecker, constante de Hadamard de La Vallée Poussin ou constante des inverses des nombres premiers) est utilisée principalement en… … Wikipédia en Français
Constante De Meissel-Mertens — En mathématiques, la constante de Meissel Mertens (également nommée dans la littérature mathématique constante de Mertens, constante de Kronecker, constante d Hadamard de la Vallée Poussin ou constante des inverses des nombres premiers) est une… … Wikipédia en Français
Constante de meissel-mertens — En mathématiques, la constante de Meissel Mertens (également nommée dans la littérature mathématique constante de Mertens, constante de Kronecker, constante d Hadamard de la Vallée Poussin ou constante des inverses des nombres premiers) est une… … Wikipédia en Français
Franz Mertens — Pour les articles homonymes, voir Mertens. Franz Mertens (20 mars 1840 5 mars 1927) est un mathématicien allemand, né à Środa Wielkopolska (actuellement en Pologne) et mort à Vienne (Autriche). Le deuxième de ses trois… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Produit de Cauchy — Pour les articles homonymes, voir Cauchy. En analyse, le produit de Cauchy est une opération portant sur certaines séries. Il permet de généraliser la propriété de distributivité. Son nom est un hommage à l analyste français Augustin Louis Cauchy … Wikipédia en Français
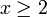 , on a :
, on a :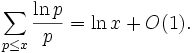
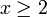 , on a :
, on a :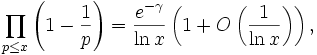
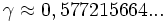 est la constante d'Euler-Mascheroni.
est la constante d'Euler-Mascheroni.