- Tablette d'argile YBC 7289
-
Tablette d'argile YBC 7289
La tablette d'argile YBC 7289 babylonienne est une pièce archéologique. Depuis 1912, elle est en possession de l'Université Yale, d'où son nom : Yale Babylonian Collection, N°7289.
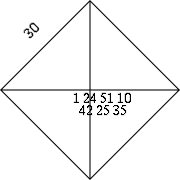
Photographie de la tablette YBC 7289 avec des annotations traduisant les nombres écrits dans le système babylonien.
(Crédit : Bill Casselman)Elle est écrite en cunéiforme. Son intérêt réside dans le fait qu'elle est la plus ancienne représentation connue de la racine carrée de deux, notée aujourd'hui √2.
Sommaire
Description
Cette tablette a la forme d'un disque d'environ 8 cm de diamètre et 8 mm d'épaisseur.
Une face représente un carré et ses diagonales. Sur un côté de ce carré, on peut lire le chiffre suivant, dans le système sexagésimal babylonien :
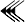
signifiant : (30) À l'intérieur, le long d'une diagonale, se trouvent les deux séries de chiffres : 
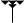
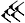
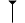
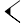
signifiant : (1, 24, 51, 10)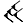 
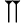
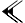
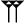
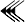
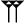
signifiant : (42, 25, 35) Histoire
YBC 7289 est datée du premier tiers du IIe millénaire av. J.-C. (-1700 ± 100). On ne connaît pas son origine exacte ; elle provient sans doute du sud de l'Irak actuel.
Elle a été achetée vers 1912 et publiée pour la première fois en 1945. Elle est actuellement conservée à l'Université Yale.
Analyse
Schéma de la tablette YBC 7289.La forme et les dimensions de la tablette laissent supposer qu'elle a été utilisée par un apprenti scribe recopiant des valeurs connues.
Le système babylonien de numération étant sexagésimal, la suite 1 ; 24 ; 51 ; 10 doit être interprétée comme 1 + 24/60 + 51/60² + 10/60³ (soit 30547/21600, notons le a) et 42 ; 25 ; 35 comme 42 + 25/60 + 35/60²(soit 30547/720, notons le b). On peut remarquer que les trois nombres qui apparaissent sur la tablette (le troisième étant c=30) sont liés par la relation b=a×c.
On peut remarquer que le nombre c est noté près d'un côté du carré, les deux autres étant situés le long d'une diagonale. D'autre part, le théorème « de Pythagore »[1] a pour conséquence que le rapport entre la diagonale b et le côté c d'un carré est égal à la racine carrée de deux. La suite 1 ; 24 ; 51 ; 10 peut donc être interprétée comme une valeur approchée de ce nombre. Une calculette nous indique que :
- 30547/21600 ≈ 1,41421296
- √2 ≈ 1,41421356
La précision du calcul de la racine carrée de deux par les Babyloniens est donc de l'ordre du millionième près, soit six décimales.
Pourquoi 30 ?
Le système de numération babylonien ne permet pas de connaître la valeur exacte d'un nombre, mais seulement celle-ci à un exposant 60 près[2]. Ainsi
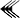peut-il signifier 30 comme 30×60, 30×60² ou 30/60, etc. Une hypothèse est que le 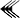qui apparait sur le côté du carré de YMC 7289 signifie 30/60, c'est-à-dire 1/2. Si c'était le cas, alors la sérieserait égale à 42/60 + 25/60² + 35/60³, soit 30547/43200, et serait donc une valeur approchée de la moitié de la racine carrée de deux (notée de nos jours √2/2). Comme ils effectuaient des divisions par multiplication par l'inverse, les mathématiciens babyloniens s'intéressaient beaucoup aux inverses des nombres. Cette hypothèse peut laisser supposer qu'ils connaissaient la relation
- 1/√2 = √2/2 = √(1/2)
Autre explication et analyse
Sans invalider les hypothèses développées ci-haut, l'explication très banale et plus simple des valeurs c et b est la suivante : c = 30 égale la valeur en doigts de la coudée, tandis que b = 42,42638 est la valeur en doigts de la diagonale de son carré. Un apprenti arpenteur les recopia.
Notes
- ↑ Remarquons au passage que les Babyloniens connaissaient ce théorème plus de mille ans avant la naissance de Pythagore.
- ↑ Cela ressemble à la notation de nos calculettes contemporaines avec mantisse et exposant. Les Babyloniens ne retenaient que la mantisse à condition qu'elle ne se termine pas par un zéro et ne notaient pas l'exposant qu'ils conservaient mentalement. En fait, vue d'un œil moderne nous dirions que les Babylionniens calculaient en virgule flottante.
Voir aussi
Liens internes
Liens externes
- (fr)Une analyse de la tablette YBC7289 sur le site BibNum (textes fondateurs de la science)
- (en) Photos de YBC 7289 de Bill Casselman (des photos de bonne qualité)
Références
- (en) J. J. O'Connor and E. F. Robertson, Le « théorème de Pythagore » dans les mathématiques babyloniennes, 2000.
- (en) David Fowler et Eleanor Robson, Square Root Approximations in Old Babylonian Mathematics : YBC 7289 in Context, dans Historia Mathematica, 25 (1998), 366–378
- (en) Otto Neugebauer et Abraham Sachs, Mathematical Cuneiform Texts, American Oriental Series, vol. 29, New Haven, 1945.
Portail des mathématiques
Portail de l’archéologie
Portail du Proche-Orient ancien
Catégories : Mathématiques de l'Antiquité | Archéologie | Tablette d'argile | Cunéiforme
Wikimedia Foundation. 2010.
