Système décimal sans zéro

Le système décimal sans zéro est un système de numération expérimental visant à montrer que l'humanité aurait pu développer un système positionnel ne faisant pas intervenir le symbole zéro.

Sommaire 1 Présentation 2 Énonciation 3 Particularités 3.1 Orales 3.2 Mathématiques 4 Conclusion

Présentation

Avec les nombres zéro (0) et infini (∞) comme cas particuliers.

Les nombres entre guillemets font référence au système standard.

1	2	3	4	5	6	7	8	9	X	avec X = "10"
11	12	13	14	15	16	17	18	19	1X	avec 1X = "20"
21	22	23	24	25	26	27	28	29	2X	avec 2X = "30"
...
91	92	93	94	95	96	97	98	99	9X	avec 9X = "100"
X1	X2	X3	X4	X5	X6	X7	X8	X9	XX	avec XX = "110"
111	112	113	114	115	116	117	118	119	11X	avec 11X = "120"
...
991	992	993	994	995	996	997	998	999	99X	avec 99X = "1000"
9X1	9X2	9X3	9X4	9X5	9X6	9X7	9X8	9X9	9XX	avec 9XX = "1010"
X11	X12	X13	X14	X15	X16	X17	X18	X19	X1X	avec X1X = "1020"
...
X91	X92	X93	X94	X95	X96	X97	X98	X99	X9X	avec X9X = "1100"
XX1	XX2	XX3	XX4	XX5	XX6	XX7	XX8	XX9	XXX	avec XXX = "1110"
1111	1112	1113	1114	1115	1116	1117	1118	1119	111X	avec 111X = "1120"

Et ainsi de suite, avec :

9 99X = "10 000"
X XXX = "11 110"
99 99X = "100 000"
XX XXX = "111 110"
999 99X = "1 000 000"
XXX XXX = "1 111 110"
9 999 99X = "10 000 000"
X XXX XXX = "11 111 110"

Nous avons donc les puissances de dix :

X*X = 9X
X*X*X = 99X
X*X*X*X = 999X
X^X = 9 999 999 99X

Énonciation

Voici un exemple d'énonciation des nombres illustrant la régularité du système au travers de ce qu'aurait pu devenir la langue française si elle avait intégré ce système :

• Les unités ne changent pas :

un, deux, trois, quatre, cinq, six, sept, huit, neuf, dix.

• Les dizaines peuvent être régularisées :

de unante-un à unante-dix, de vingt-un à vingt-dix, de trente-un à trente-dix, de quarante-un à quarante-dix, de cinquante-un à cinquante-dix, de soixante-un à soixante-dix, de septante-un à septante-dix, de octante-un à octante-dix, de nonante-un à nonante-dix, et de décante-un à décante-dix.

• Les centaines commencent à 111 :

de cent-unante-un à dix-cent-décante-dix (XXX).

• Les milliers commencent à 1 111, jusqu'à XXX XXX :

de mille-cent-unante-un à dix-cent-décante-dix-mille-dix-cent-décante-dix.

• Et ainsi de suite avec les millions et milliards.

Particularités

Orales

• Les puissances de dix sont plus longues à énoncer que dans le système actuel, sans gain inverse compensatoire dans la numération, ce qui ajoute à la difficulté du système.

• Certains termes utilisés dans la numération ne définissent pas, isolément, des nombres : « unante », « vingt », « décante », « cent », « mille », etc. ne constituent des nombres qu'avec d'autres termes leur faisant suite. En leur absence, cette restriction leur permet cependant d'exprimer des intervalles de nombres ; si « unante-dix » est un nombre, « vingt » peut alors être employé pour désigner les nombres de « vingt-un » à « vingt-dix ». Cela, d'une part, est formellement satisfaisant, et conforme à l'usage, car dans « les années mille-neuf-cent », à « mille-neuf-cent » ne correspond pas un nombre, mais bien un intervalle de nombres ; et, d'autre part, permet de remplacer des périphrases, « mille-neuf-cent » étant plus concis que « la dernière centaine du millier » ou que « mille-neuf-cent quelque chose ».

• Une même valeur peut être représentée par différents termes au cours de la numération (dix = unante, cent = décante, mille = dix cents, etc.). Cependant, si chacun de ces doublons exprime bien une même valeur au sein d'un nombre, leur emploi diffère, comme indiqué en présentation et au point précédent.

Mathématiques

Ce système ne représente pas les nombres en développement décimal :

• Deux chiffres distincts peuvent, à une position différente, représenter la même valeur : dans l'écriture 1X, 1 et X comptabilisent tous les deux dix unités.

• L'augmentation d'un chiffre n'indique pas le dépassement d'une puissance de dix : X² < X1 < 111 < X³.

• L'écriture d'un nombre ne correspond pas à sa décomposition en puissances de dix : 4X1 = 5.X² + 1.

De ce fait, la virgule pose problème :

• Avec la virgule, les nombres ne bénéficient pas d'une représentation unique : 3 = 2,X = 2,9X.

• Le classement ordonné des nombres dans leur écriture n'utilisant pas la même quantité de chiffres après la virgule est peu intuitif : 3,9 < 4 < 3,9X1.

• La virgule ne permet pas de représenter tous les nombres rationnels : 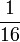ne peut pas s'écrire avec une virgule sans l'intervention d'un zéro positionnel.

La virgule est donc inutilisable. Les nombres fractionnaires doivent être représentés par une autre notation, moins compacte, faisant intervenir une barre de fraction ou la multiplication par une puissance de dix négative.

Conclusion

Ce système, grâce à son principe positionnel, est nettement plus performant qu'un système additif, telle la numération romaine. Cependant, son intérêt est surtout de donner un éclairage quant à l'importance du chiffre zéro et à la nature de cette importance, car, si l'invention de ce chiffre n'a rien d'une étape obligatoire dans le développement d'un système numérique positionnel, les propriétés qui découlent de l'utilisation de ce dernier rendent le système simple et élégant. Aussi, la représentation des nombres en développement décimal est pratique et parfaitement légitime.