Symbole de hilbert

Symbole de hilbert

Symbole de Hilbert

En mathématiques, le symbole de Hilbert, nommé d'après le mathématicien allemand de la fin du XIXe et du début du XXe siècles, David Hilbert, est une application algébrique permettant de tester les solutions de certaines équations algébriques, particulièrement dans les corps de nombres p-adiques, mais aussi un objet permettant de formuler certaines lois de réciprocité, et intéressant pour la théorie des corps de classes ; enfin, c'est un cas particulier de la notion de symbole sur un corps, qui est un concept important en K-théorie.

La première définition est basée sur le fait que tout corps de nombres p-adiques contient les racines 2e de l'unité. Le symbole de Hilbert (x,y)2 de deux éléments non nuls x et y du corps K considéré est alors 1 ou -1 suivant que l'équation α2y + β2x = 1 admet ou non une solution (α,β) dans le corps K. 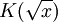Une telle équation revient en fait à se demander si y est une norme dans l'équation a priori quadratique K(\sqrt{x}).

Cette définition se généralise en un symbole à valeurs dans le groupe des racines de l'unité du corps considéré. Avec ce point de vue, en considérant tous les symboles de Hilbert définis sur les différents corps de nombres p-adiques \mathbb{Q}_p on parvient à une formulation de la loi de réciprocité quadratique, et plus généralement à la loi de réciprocité pour les puissances n-èmes pour un corps de nombres dont le groupe des racines de l'unité est un multiple de n.

Référence

  • (en) Georges Gras, Class Field Theory : From Theory to Practice [détail des éditions]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Symbole de Hilbert ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Symbole de hilbert de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Symbole de Hilbert — En mathématiques, le symbole de Hilbert, nommé d après le mathématicien allemand de la fin du XIXe et du début du XXe siècles, David Hilbert, est une application algébrique permettant de tester les solutions de certaines équations algébriques,… …   Wikipédia en Français

  • HILBERT (PROBLÈMES DE) — «Qui ne se réjouirait de pouvoir soulever le voile qui cache le futur, de jeter un regard sur le développement des mathématiques, ses progrès ultérieurs, les secrets des découvertes des siècles à venir?...» Prévoir le futur des mathématiques: qui …   Encyclopédie Universelle

  • HILBERT (D.) — Le mathématicien allemand David Hilbert a ouvert la voie à plusieurs générations de chercheurs et a joué un rôle important dans l’élaboration des idées, non seulement dans sa spécialité, mais dans le cadre d’une réflexion générale sur la science …   Encyclopédie Universelle

  • Hilbert — David Hilbert David Hilbert David Hilbert en 1912 Naissance 23 janvier 1862 Königsberg (Prusse Orientale) …   Wikipédia en Français

  • David Hilbert — en 1912 Naissance 23 janvier 1862 Königsberg (Prusse Orientale) Décès 14 février 1943 …   Wikipédia en Français

  • Corps De Hilbert — Corps de classes de Hilbert En théorie algébrique des nombres, le corps de Hilbert H(K) d un corps de nombres algébriques K est l extension abélienne non ramifiée maximale de ce corps de nombres. Cet objet doit son nom au mathématicien allemand… …   Wikipédia en Français

  • Corps de Hilbert — Corps de classes de Hilbert En théorie algébrique des nombres, le corps de Hilbert H(K) d un corps de nombres algébriques K est l extension abélienne non ramifiée maximale de ce corps de nombres. Cet objet doit son nom au mathématicien allemand… …   Wikipédia en Français

  • Corps de hilbert — Corps de classes de Hilbert En théorie algébrique des nombres, le corps de Hilbert H(K) d un corps de nombres algébriques K est l extension abélienne non ramifiée maximale de ce corps de nombres. Cet objet doit son nom au mathématicien allemand… …   Wikipédia en Français

  • Corps de classes de Hilbert — En théorie algébrique des nombres, le corps de Hilbert H(K) d un corps de nombres algébriques K est l extension abélienne non ramifiée maximale de ce corps de nombres. Cet objet doit son nom au mathématicien allemand David Hilbert. Son étude est… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”