- Automate À Pile
-
Automate à pile
Un automate à pile est une machine abstraite utilisée en informatique théorique et, plus précisément, en théorie des automates. Un automate à pile est semblable à un automate fini non-déterministe mais il dispose également d'une pile qui peut être utilisée pour stocker des informations pertinentes. La puissance de calcul des automates à piles correspond aux langages non-contextuels soit ceux qui peuvent être décrits par une grammaire hors-contexte.
Sommaire
Utilisation
Les automates à pile utilisent une zone de mémoire organisée en pile, qui permet de sauver des informations.
- Le choix d'une transition peut dépendre de la valeur au sommet de la pile (pop)
- Une transition peut entraîner un ou plusieurs empilements (push).
Définitions formelles
Un automate à pile est un 7-uplet
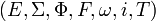, où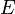
est l'ensemble d'états,
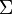est l'alphabet d'entrée,
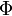est l'alphabet de pile,
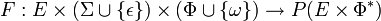est la relation de transition,
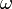est le symbole de pile vide,
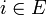est l'état initial,
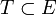est l'ensemble des états terminaux.
Fonctionnement
L'automate commence à l'état i. La transition s'effectue en appliquant F(q,a,p) = (q1',P1),...,(qn',Pn) où q est un des états courant, a est le caractère lu, p est un élément de la pile qui sera dépilé (peut être ω), qk' est un des nouveaux états dans lequel peut passer l'automate en empilant Pk. L'automate accepte le mot s'il a la possibilité, en lisant tout le mot, d'arriver dans un des états finaux.
Exemples
Reconnaissance du langage
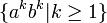
On peut utiliser l'automate
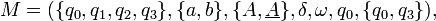
où les transitions sont définies par :
(1)
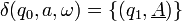
(2)
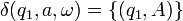
(3)
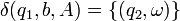
(4)
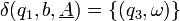
(5)
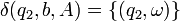
(6)
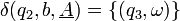
(7)
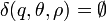pour les autres valeurs de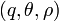 
Par exemple, dans l'état
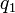, si on lit un 
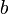et que l'on dépile un 
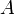, on passe dans l'état 
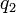sans rien empiler.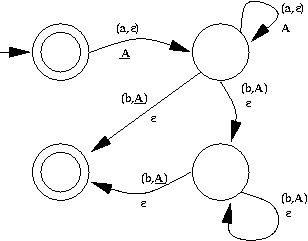
On commence par lire le premier caractère : Si le mot est vide on a fini et le mot est accepté car q0 est un état final. Si c'est un a, on empile
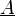(1) (il marque le fond de la pile), et on passe à l'état q1. Si c'est un b, le mot est rejeté (7).Ensuite dans l'état q1, à chaque a on empile A (2). Si on a un b, deux possbilités : - Si on n'a empilé qu'un seul
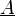on passe à l'état q3 en dépilant le 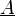(4). - Si on a empilé un ou plus A, on passe à l'état q2 en dépilant un A (3).Dans l'état q2, si on a un b, soit on dépile un A et on reste dans cet état (5), soit on dépile un
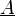(fond de la pile) et on passe dans l'état q3 (6). Si on lit un a, on désactive l'automate et le mot est rejeté (7).Dans l'état q3, si le mot est fini on l'accepte car
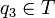, si non on le rejete (7).Propriétés
Chaque langage défini par une grammaire non contextuelle est reconnu par un automate à pile et réciproquement.
En conséquence, le problème de l'appartenance d'un mot à un langage non contextuelle est décidable : il existe un algorithme qui, étant donnés la description d'une grammaire non contextuelle et un mot, répond en temps fini à la question de l'appartenance de ce mot au langage défini par cette grammaire.
Implémentation d'un automate à pile
-
#include <stdlib.h> -
#include <stdio.h> -
-
#define POP -1 -
#define ACCEPT -2 -
#define ERROR -3 -
-
#define ALPHABET 3 /* Grandeur*/ -
-
/* -
Push-down automation) -
-
Symbol | ( | ) | \0 -
---------+---------+--------+----------- -
State 0 | PUSH 1 | ERROR | ACCEPT -
State 1 | PUSH 1 | POP | ERROR -
*/ -
-
int states[2][ALPHABET*2] =
-
{ -
{ -
'(', 1 /* PUSH 1 */,
-
')', ERROR,
-
'\0', ACCEPT
-
},
-
{ -
'(', 1 /* PUSH 1 */,
-
')', POP,
-
'\0', ERROR
-
} -
};
-
-
-
int main( int argc, char** argv )
-
{ -
int stack[100] = { 0 };
-
int i = 0;
-
int action = 0;
-
int* tos = stack;
-
char s [80+1];
-
char* p = s;
-
-
/* Chaine de donnée */ -
printf("Entrez l'expression: ");
-
gets( &s );
-
-
/*Pile poussée*/ -
*(tos++) = 0;
-
-
/* Sortie */ -
do -
{ -
/* Boucle*/ -
action = ERROR;
-
for( i = 0; i < ALPHABET; i++ )
-
{ -
if( states[*(tos-1)][i*2] == *p )
-
{ -
action = states[*(tos-1)][i*2+1];
-
break;
-
} -
} -
-
/* Actions*/ -
if( action == ERROR )
-
{ -
printf("Erreur innatendue à la position %d", p-s);
-
break;
-
} -
else if( action == ACCEPT )
-
printf("Sortie acceptée!");
-
else if( action == POP )
-
tos--; -
else -
*(tos++) = action;
-
-
/* Données supplémentaires... */ -
p++; -
} -
while( action != ACCEPT );
-
-
getchar();
-
return 0;
-
}
Voir aussi
Références
- (fr) Olivier Carton, Langages formels, calculabilité et complexité. Vuibert 2008, (ISBN 978-2-7117-2077-4).
Portail des mathématiques
Portail de l’informatique
Catégories : Langage formel | Calculabilité
Wikimedia Foundation. 2010.
