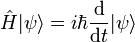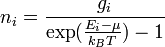Statisitique de Bose-Einstein

Pour les articles homonymes, voir Einstein (homonymie).

Cet article fait partie de la série Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

En mécanique quantique et en physique statistique, la statistique de Bose-Einstein désigne la distribution statistique de bosons indiscernables (tous similaires) sur les états d'énergie d'un système à l'équilibre thermodynamique. La distribution en question résulte d'une particularité des bosons : les particules de spin entier ne sont pas assujetties au principe d'exclusion de Pauli, à savoir que plusieurs bosons peuvent occuper simultanément un même état quantique.

Distribution de Bose-Einstein

La statistique de Bose-Einstein a été introduite par Satyendranath Bose en 1920 pour les photons et généralisée aux atomes par Albert Einstein en 1924. Statistiquement, à l'équilibre thermodynamique, le nombre n_i de particules d'énergie E_i est

où :

• g_i est la dégénérescence du niveau d'énergie E_i, à savoir le nombre d'états possédant cette énergie ;
• μ est le potentiel chimique ;
• k_B est la constante de Boltzmann ;
• T est la température.

Limite classique et comparaison avec les fermions

À haute température, lorsque les effets quantiques ne se font plus sentir, la statistique de Bose-Einstein, comme la statistique de Fermi-Dirac qui régit les fermions, tend vers la statistique de Maxwell-Boltzmann. Aux basses températures, cependant, les deux statistiques diffèrent entre elles. Ainsi, à température nulle :

• avec la statistique de Bose-Einstein, le niveau de plus basse énergie contient tous les bosons;
• avec la statistique de Fermi-Dirac, les niveaux de plus basse énergie contiennent chacun au plus g_i fermions.

Condensat de Bose-Einstein

Comme vu précédemment, la statistique de Bose-Einstein prévoit qu'à température nulle, toutes les particules occupent le même état quantique, celui de plus basse énergie. Ce phénomène est observable à l'échelle macroscopique et constitue un condensat de Bose-Einstein.

Voir également

• Autres distributions statistiques en mécanique quantique
  • en mécanique quantique : statistique de Fermi-Dirac
  • en mécanique classique : statistique de Maxwell-Boltzmann
• physique statistique
• physique quantique

• Portail de la physique