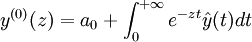Sommabilité de Borel
- Sommabilité de Borel
-
Sommation de Borel
En mathématiques, la sommation de Borel est une généralisation de la notion usuelle de sommation d'une série. En particulier, elle donne une définition d'une grandeur qui se comporte en de nombreux aspects comme la somme, même lorsque la série est divergente. Ce concept est notamment très utile en théorie des perturbations, une branche des mathématiques très utilisée dans les calculs de physiques. Ce procédé de sommation fut d'abord étudié par le mathématicien Émile Borel.
Definition
Soit y la série formelle des puissances de z :
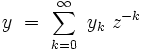
On définit la transformée de Borel 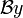 de y par :
de y par :
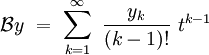
Supposons alors que :
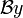 possède un rayon de convergence non nul comme fonction de t ;
possède un rayon de convergence non nul comme fonction de t ;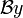 peut être prolongée analytiquement en une fonction
peut être prolongée analytiquement en une fonction 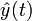 sur la droite réelle positive ;
sur la droite réelle positive ;- la fonction
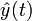 croit au plus exponentiellement sur la droite réelle positive.
croit au plus exponentiellement sur la droite réelle positive.
Alors, y est dite Borel-sommable, et la somme de Borel de y est donnée par la transformée de Laplace de la fonction 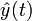 ; cette transformée existe compte-tenu de la condition (3) ci-dessus
; cette transformée existe compte-tenu de la condition (3) ci-dessus
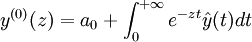
Remarque
La transformation de Borel n'est autre que la série obtenue en appliquant une transformée de Laplace inverse terme à terme à la série initiale. Lorsque le calcul des transformées de Laplace peut se faire terme à terme, la sommation au sens de Borel donne le même résultat que la sommation usuelle des séries. Mais la somme de Borel est définie dans de nombreux cas où cette dernière ne l'est pas.
Voir aussi
Articles connexes
Liens externes
 Portail des mathématiques
Portail des mathématiques Portail de la physique
Portail de la physique
Catégories : Série | Physique mathématique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Sommabilité de Borel de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
BOREL (É.) — Grand mathématicien, mais aussi homme politique et philosophe, Émile Borel laisse une œuvre scientifique très variée. Son talent s’exprime dans l’art d’ouvrir des voies nouvelles, d’y faire des premiers pas, assez importants pour attirer… … Encyclopédie Universelle
Méthode de sommation — Série divergente En mathématiques, une série infinie est dite divergente si la suite de ses sommes partielles n est pas convergente. En ce qui concerne les séries de nombres réels, ou de nombres complexes, une condition nécessaire de convergence… … Wikipédia en Français
Serie divergente — Série divergente En mathématiques, une série infinie est dite divergente si la suite de ses sommes partielles n est pas convergente. En ce qui concerne les séries de nombres réels, ou de nombres complexes, une condition nécessaire de convergence… … Wikipédia en Français
Calcul des perturbations — Théorie des perturbations D un point de vue heuristique, la théorie des perturbations est une méthode mathématique générale qui permet de trouver une solution approchée d une équation mathématique (Eλ) dépendante d un paramètre λ lorsque la… … Wikipédia en Français
Theorie des perturbations — Théorie des perturbations D un point de vue heuristique, la théorie des perturbations est une méthode mathématique générale qui permet de trouver une solution approchée d une équation mathématique (Eλ) dépendante d un paramètre λ lorsque la… … Wikipédia en Français
Théorie des perturbations — D un point de vue heuristique, la théorie des perturbations est une méthode mathématique générale qui permet de trouver une solution approchée d une équation mathématique (Eλ) dépendante d un paramètre λ lorsque la solution de l équation (E0),… … Wikipédia en Français
1 − 2 + 3 − 4 + · · · — Série alternée des entiers Les premiers milliers de termes et de sommes partielles de 1 − 2 + 3 − 4 + … La série alternée des entiers est, en mathématiques, la série associée à la suite des nombres entiers (strictement positifs), affectés de… … Wikipédia en Français
Série alternée des entiers — Traduction à relire 1 − 2 + 3 − 4 … Wikipédia en Français
Série lacunaire — En mathématiques, et plus précisément en analyse, une série lacunaire (aussi connue sous le nom de fonction lacunaire) est une série entière (ou la fonction somme de cette série entière) présentant des lacunes, c est à dire dont un grand nombre… … Wikipédia en Français
Série divergente — En mathématiques, une série infinie est dite divergente si la suite de ses sommes partielles n est pas convergente. En ce qui concerne les séries de nombres réels, ou de nombres complexes, une condition nécessaire de convergence est que le terme… … Wikipédia en Français
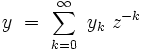
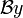 de y par :
de y par :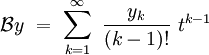
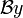 possède un rayon de convergence non nul comme fonction de t ;
possède un rayon de convergence non nul comme fonction de t ;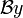 peut être prolongée analytiquement en une fonction
peut être prolongée analytiquement en une fonction 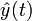 sur la droite réelle positive ;
sur la droite réelle positive ;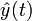 croit au plus exponentiellement sur la droite réelle positive.
croit au plus exponentiellement sur la droite réelle positive.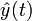 ; cette transformée existe compte-tenu de la condition (3) ci-dessus
; cette transformée existe compte-tenu de la condition (3) ci-dessus