Singularité éliminable

Singularité éliminable

Singularité en analyse complexe

En analyse complexe à une variable, une singularité d'une fonction f est un point z sur le voisinage apointé duquel la fonction f est définie et holomorphe. Autrement dit, on dispose d'une fonction f d'une variable complexe régulière (= holomorphe) définie sur un ouvert U du plan complexe C ; une singularité de f est un point isolé du bord de U. Le premier paragraphe clarifie la définition.

Les singularités se classent en trois types : singularités effaçables, pôles, et singularités essentielles.

Sommaire

Définition détaillée

Augustin Louis Cauchy

Une fonction holomorphe est une fonction f d'une variable complexe, définie et dérivable sur un ouvert U. Une telle fonction est développable en séries entières au voisinage de chaque point de U: ce premier résultat révèle la rigidité qui caractérise l'analyse complexe. Il peut être intéressant de s'intéresser au comportement de f sur le bord de U.

Une singularité de f est un point isolé du bord de U. Étudier les singularités d'une fonction holomorphe, c'est étudier le comportement de f en les points isolés du bord de U.

Un voisinage apointé de Z est un voisinage de Z privé de Z. Cette définition permet de caractériser les points isolés du bord:

Un nombre complexe Z est un point isolé du bord de U si et seulement si U est un voisinage apointé de Z.

On peut donc redéfinir les singularités de f comme les nombres complexes au voisinage apointé desquels f définit une fonction holomorphe. Pour des raisons pratiques et calculatoires, de nombreux auteurs se placent directement sur un "disque apointé".

Un disque apointé D en Z est un disque centré en Z privé du point Z. Autrement dit, D est l'ensemble des nombres complexes z tels que 0<|z-Z|<r où r est le rayon du disque apointé. Bien sûr, un disque apointé est un cas particulier de voisinage apointé.

Classification

Singularité effaçable

Une singularité Z d'une fonction holomorphe est effaçable si f se prolonge au voisinage de Z en une fonction holomorphe. Autrement dit, on peut effacer la singularité Z, l'oublier, et penser f comme une fonction holomorphe définie au voisinage de Z.

La singularité Z de f est effaçable si et seulement si f est une fonction bornée sur un voisinage apointé de Z.

En particulier, un prolongement continu g de f en une singularité est nécessairement une fonction holomorphe. En effet, l'existence d'un prolongement continu de f implique que f est bornée sur tout voisinage apointé suffisamment petit de Z. Par conséquent, la singularité Z est effaçable, ce qui signifie que f admet un prolongement holomorphe h en Z. Comme toute fonction holomorphe est continue, la fonction h est aussi un prolongement continu de f en Z et donc coïncide avec g. En particulier, g=h est holomorphe.


Preuve de l'équivalence
On peut supposer Z=0 et se placer sur le disque apointé D' en 0 de rayon r. On considère donc une fonction f holomorphe sur D'.
Sens direct
Si f se prolonge en 0 (prolongement holomorphe), alors le prolongement de f est en particulier une fonction continue sur le disque D de centre 0 et de rayon r. Le disque fermé de centre 0 et de rayon r/2 est un compact, en restriction duquel le prolongement est borné. Par conséquent la fonction f prend des valeurs bornées sur le disque apointé de centre 0 et de rayon r/2.
Sens réciproque
Réciproquement, supposons que f est bornée sur un voisinage apointé de 0. Quitte à restreindre r, la fonction f est supposée bornée sur le disque apointé D'. On définit une fonction auxiliaire g par:
g(z) = z2f(z).
A priori, g est une fonction holomorphe sur le disque apointé D'. Comme f est bornée, g(z) est négligeable devant z. Par conséquent, g se prolonge par continuité en 0 en une fonction d'une variable complexe ; et le prolongement, noté abusivement g, est dérivable. Plus précisément, la fonction g et sa dérivée s'annulent en 0.
Donc, g est une fonction holomorphe sur le disque D de centre 0 et de rayon r. Par conséquent, elle est développable en séries entières en 0:
g(z)=\sum_{n\geq 2}\frac{g^{(n)}(0)}{n!}z^n
La série entière converge normalement sur voisinage compact de 0. Par division par z2, on trouve immédiatement:
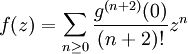
f(z)=\sum_{n\geq 0}\frac{g^{(n+2)}(0)}{(n+2)!}z^n
Donc, sur un voisiange apointé de 0, f coïncide avec la somme d'une série entière. Par conséquent, f se prolonge en une fonction holomorphe en 0.

L'exemple est la fonction z\in \C^* \mapsto \sin z/z \in \C.

Pôle

La singularité Z est appelée un pôle de f si :

  • La singularité est non effaçable ;
  • Et pour n suffisamment grand, la fonction 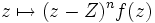z\mapsto (z-Z)^nf(z) se prolonge en une fonction holomorphe en Z.

Le plus petit entier n possible est appelé l'ordre du pôle Z.

Une singularité Z de f est un pôle si et seulement si f converge en l'infini en Z.


Preuve de l'équivalence
Comme ci-dessus, on suppose Z  =  0, et on regarde la fonction f sur le disque apointé D' de centre 0 et de rayon r.
Sens direct
Notons N l'ordre du pôle 0 de f. Alors, g(z) = zNf(z) se prolonge en une fonction holomorphe en 0, qui ne s'annule pas en 0[précision nécessaire]. En particulier, f équivaut en 0 à 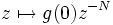z\mapsto g(0)z^{-N}. Donc, en particulier, f tend vers l'infini en 0.
Sens réciproque
Comme f tend vers l'infini en 0, la fonction f ne s'annule pas au voisinage de 0. Quitte à restreindre r, on peut supposer, sans perte de généralité, que g=1/f est bien définie sur le disque apointé D'. C'est une fonction holomorphe sur le disque apointé D', et qui se prolonge par continuité en 0 par la valeur g(0)=0. Par ce qui précède, le prolognement g est une fonction holomorphe qui s'annule en 0.
Posons N l'ordre de 0 comme zéro de la fonction holomorphe g. Au voisinage de 0, g s'écrit : g(z)=zNh(z), où h est une fonction holomorphe qui ne s'annule pas en 0. L'inverse k=1/h est une fonction définie et holomorphe au voisinage de 0.
Il s'en suit:
zNf(z) = k(z)
Par conséquent, 0 est un pôle de f ; et à ce stade, il ne serait pas difficile de prouver que N est l'ordre du pôle!

Les fractions rationnelles sont des exemples typiques de fonctions présentant des pôles. On peut aussi citer les célèbres fonctions gamma d'Euler et zêta de Riemann qui présentent toutes les deux des pôles.

Singularité essentielle

La singularité Z est essentielle dans tous les autres cas. Le comportement de f au voisinage apointé de Z est dans ce cas très compliqué. En particulier, on peut citer le théorème de Weierstrass-Casorati et les deux théorèmes de Picard.

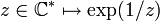L'exemple classique est la fonction z \in \C^* \mapsto \exp(1/z).

Série de Laurent

Article détaillé : série de Laurent.

Si f est une fonction holomorphe sur un disque apointé D de centre a et de rayon r, il existe une unique suite de complexes 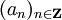(a_n)_{n\in \mathbf{Z}} telle que sur D:

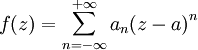f(z)=\sum_{n=-\infty}^{+\infty} a_n{(z-a)}^n,

où la série converge normalement sur tout compacte du disque apointé D.

On peut lire la nature de la singularité sur les coefficients an:

Relation série de Laurent/singularité
Nature de la singularité Information sur les coefficients de la série de Laurent
Singularité effaçable Les coefficients an sont nuls pour les indices n<0
Pôle d'ordre k Les coefficients an sont nuls pour les indices n<-k
Singularité essentielle Il existe une infinité d'indices négatifs -n pour lesquels a-n est non nul

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Singularit%C3%A9 en analyse complexe ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Singularité éliminable de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”