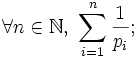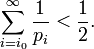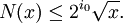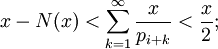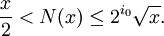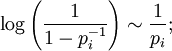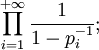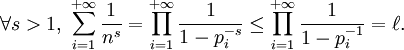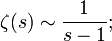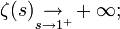Serie des inverses des nombres premiers

Serie des inverses des nombres premiers

Série des inverses des nombres premiers

En mathématiques, la série des inverses des nombres premiers est définie par

\forall n \in \N,\ \sum_{i=1}^n \frac{1}{p_i};

où pi désigne le i-ème nombre premier.

Étant donné qu'il existe une infinité de nombres premiers, cette suite n'est pas constante à partir d'un certain rang. Cependant, elle n'est pas convergente pour autant. Et comme elle est strictement croissante, cette suite diverge vers l'infini.

Sommaire

Preuve par l'analyse

Supposons par l'absurde que la série des inverses des nombres premiers soit convergente. Il existe donc un nombre entier suffisamment grand i0 tel que:

\sum_{i=i_0}^\infty \frac{1}{p_i}< \frac{1}{2}.

Définissons N(x) comme le nombre d'entiers strictement positifs inférieurs à x et qui ne sont pas divisibles par un nombre premier autre que les i0 premiers. Un tel entier peut être écrit sous la forme km2 où k est entier sans facteur carré.

Puisque seulement les i0 premiers nombres premiers pourraient diviser k, il y a au plus 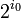2^{i_0} choix pour k. Conjointement avec le fait qu'il y a au plus 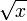\sqrt{x} valeurs possibles pour m, cela nous donne:

N(x) \leq 2^{i_0}\sqrt{x}.

Le nombre d'entiers strictement positifs inférieurs à x et divisibles par un nombre premier différent des i0 premiers est égal à x − N(x).

Puisque le nombre d'entiers inférieurs à x et divisible par p est au plus x / p, nous obtenons:

x - N(x) < \sum_{k=1}^\infty{x\over p_{i+k}} < {x \over 2};

ou encore

{x \over 2} < N(x) \le 2^{i_0}\sqrt{x}.

Mais cela est impossible pour tout x supérieur à 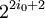2^{2i_0+2} . D'où une contradiction.

Preuve par un produit eulérien

Article détaillé : produit eulérien.

Supposons par l'absurde que la série des inverses des nombres premiers soit convergente. Comme on a l'équivalence

\log\left( \frac{1}{1-p_i^{-1}} \right) \sim \frac{1}{p_i};

on en déduit que

\prod_{i=1}^{+\infty} \frac{1}{1-p_i^{-1}};

converge vers un réel \ell. D'après le produit eulérien, on a

\forall s>1,\ \sum_{i=1}^{+\infty} \frac{1}{n^s}=\prod_{i=1}^{+\infty} \frac{1}{1-p_i^{-s}} \leq \prod_{i=1}^{+\infty} \frac{1}{1-p_i^{-1}}=\ell.

Une comparaison série-intégrale montre que lorsque 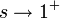s \rightarrow 1^+, on a l'équivalence

\zeta(s) \sim \frac{1}{s-1};

donc

\zeta(s) \underset{ s \rightarrow 1^+}{\rightarrow} +\infty;

ce qui est absurde.

Voir aussi

Lien externe

  • (en) Chris K. Caldwell: «Il existe une infinité de nombres premiers, mais, quelle est la grandeur de cet infini ?», [1]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « S%C3%A9rie des inverses des nombres premiers ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Serie des inverses des nombres premiers de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Série des inverses des nombres premiers — En mathématiques, la série des inverses des nombres premiers est la série de terme général 1⁄pi où pi désigne le i ème nombre premier. Le terme général de la série tend vers zéro, cependant, la suite (croissante) des sommes partielles n est pas… …   Wikipédia en Français

  • Démonstration que la série des inverses des nombres premiers diverge — Série des inverses des nombres premiers En mathématiques, la série des inverses des nombres premiers est définie par où pi désigne le i ème nombre premier. Étant donné qu il existe une infinité de nombres premiers, cette suite n est pas constante …   Wikipédia en Français

  • Conjecture Des Nombres Premiers Jumeaux — Nombres premiers jumeaux En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers qui ne diffèrent que de deux. Hormis pour la paire (2, 3), cette distance de deux est la plus petite distance possible entre deux nombres premiers …   Wikipédia en Français

  • Conjecture des nombres premiers jumeaux — Nombres premiers jumeaux En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers qui ne diffèrent que de deux. Hormis pour la paire (2, 3), cette distance de deux est la plus petite distance possible entre deux nombres premiers …   Wikipédia en Français

  • Caractérisation des nombres premiers — Nombre premier 7 est un nombre premier car il admet exactement deux diviseurs positifs …   Wikipédia en Français

  • Nombres Premiers Jumeaux — En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers qui ne diffèrent que de deux. Hormis pour la paire (2, 3), cette distance de deux est la plus petite distance possible entre deux nombres premiers. Les plus petits nombres …   Wikipédia en Français

  • Nombres premiers — Nombre premier 7 est un nombre premier car il admet exactement deux diviseurs positifs …   Wikipédia en Français

  • Nombres premiers jumeaux — En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers qui ne diffèrent que de 2. Hormis pour la paire (2, 3), cette distance de 2 est la plus petite distance possible entre deux nombres premiers. Les plus petits nombres… …   Wikipédia en Français

  • Conjecture des jumeaux premiers — Nombres premiers jumeaux En mathématiques, deux nombres premiers jumeaux sont deux nombres premiers qui ne diffèrent que de deux. Hormis pour la paire (2, 3), cette distance de deux est la plus petite distance possible entre deux nombres premiers …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”