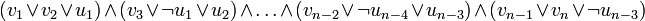SAT (problème)

Problème SAT

On nomme problème SAT un problème de décision visant à savoir s'il existe une solution à une série d'équations logiques données. En termes plus précis : une valuation sur un ensemble de variables propositionnelles^[1] telle qu'une formule propositionnelle donnée soit alors logiquement vraie. Ce problème est très important en théorie de la complexité et a de nombreuses applications en planification classique, model checking, diagnostic, et jusqu'au configurateur d'un simple PC ou de son système d'exploitation.

Sommaire

1 Définitions
- 1.1 Clause et forme clausale
- 1.2 Le problème SAT
2 Complexité et restrictions
- 2.1 NP-complétude
- 2.2 Le problème 2-SAT
3 Algorithmes de SAT
4 Applications
5 Voir aussi
6 Bibliographie
7 Notes

Définitions

Clause et forme clausale

Une clause est une proposition de la forme 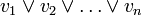$v_{1} \lor v_{2} \lor \ldots \lor v_{n}$ où les $v i$ sont des littéraux (positifs ou négatifs). Une clause d'ordre n est donc une disjonction d'au plus n littéraux. Une formule du calcul propositionnel est en forme normale conjonctive (ou forme clausale) d'ordre n si elle est une conjonction de clauses d'ordre n.

Le problème SAT

Soit une formule logique sous forme normale conjonctive (CNF). Cette CNF est satisfaisable^[2] s'il est possible d'associer une valeur logique booléenne à chacune de ses variables de telle manière que cette formule soit logiquement vraie. Déterminer si une formule sous CNF d'ordre n est satisfaisable est appelé problème de satisfaisabilité ou problème SAT d'ordre n (n-SAT). Si la formule propositionnelle n'est pas sous CNF, il est nécessaire de la normaliser^[3] pour que le problème soit qualifié de SAT. Généralement, la réponse à cette question fournit également un exemple d'assignation des variables tel que la CNF soit logiquement vrai.

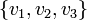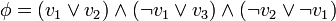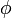Exemple: Soit l'ensemble de variables $\{v_1,v_2,v_3\}\$ et $\phi = (v_1 \lor v_2) \land (\neg v_1 \lor v_3) \land (\neg v_2 \lor \neg v_1)$ .; $\phi\$ est satisfaisable puisque, si on pose 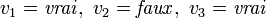$v_1 = \mathit{vrai},\ v_2 = \mathit{faux},\ v_3 = \mathit{vrai}$ , alors 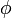$\phi\$ est logiquement vrai.; En revanche, 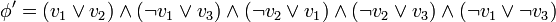$\phi' = (v_1 \lor v_2) \land (\neg v_1 \lor v_3) \land (\neg v_2 \lor v_1) \land (\neg v_2 \lor v_3) \land (\neg v_1 \lor \neg v_3)$ n'est pas satisfaisable !

Complexité et restrictions

NP-complétude

Le problème SAT est un problème NP–complet d'après le théorème de Cook. Donc de la même manière, le problème 3–SAT est lui aussi NP–complet. Pour le démontrer, il suffit de prouver que le problème SAT est polynomialement réductible à 3–SAT.

Preuve

On remarque que toute clause 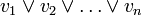$v_{1} \lor v_{2} \lor \ldots \lor v_{n}$ peut se mettre sous la forme :

$(v_{1} \lor v_{2} \lor u_{1}) \land (v_{3} \lor \lnot u_{1} \lor u_{2}) \land \ldots \land (v_{n-2} \lor \lnot u_{n-4} \lor u_{n-3}) \land (v_{n-1} \lor v_{n} \lor \lnot u_{n-3})$

Donc le problème SAT est polynomialement réductible à 3–SAT. On conclut que 3–SAT est NP–complet.

Tous les problèmes n–SAT avec n supérieur ou égal à 3 sont des problèmes NP–complets.

Exemple: Soient 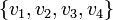$\left\{ v_1, v_2, v_3, v_4 \right\}$ des variables propositionnelles.; Déterminer si l'expression 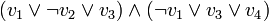$(v_1 \lor \neg v_2 \lor v_3) \land (\neg v_1 \lor v_3 \lor v_4)$ est satisfaisable est un problème 3–SAT.; Tout algorithme capable de résoudre un problème 3–SAT (même le « meilleur ») peut dans certains cas devoir essayer un nombre de combinaisons d'assignations exponentiel en la valeur $n$ .

Le problème 2-SAT

2-SAT, d'après la définition, cherche à déterminer la satisfaisabilité d'une formule F du calcul propositionnel en forme normale conjonctive d'ordre 2. Ce problème n'est pas NP-complet mais de classe 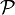$\mathcal{P}$ . Il existe plusieurs algorithmes polynomiaux pour résoudre le problème 2-SAT.

Exemple: Intéressons nous plus particulièrement à celui présenté par Aspvall, Plass et Tarjan en 1979^[4].

Une clause d'ordre deux 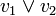$v_1 \lor v_2$ est équivalente aux implications 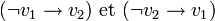$(\lnot v_1 \rightarrow v_2) \text{ et } (\lnot v_2 \rightarrow v_1)$ . Pour résoudre 2-SAT on construit le graphe orienté G = (S,A) dual (appelé graphe 2-SAT) selon les règles suivantes. Les sommets S correspondent aux différentes variables propositionnelles (ou leurs négations) de la formule considérée. 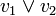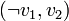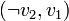On associe ensuite à chaque clause $v_1 \lor v_2$ les deux arcs $(\lnot v_1,v_2)$ et $(\lnot v_2,v_1)$ pour former l'ensemble A.

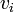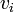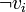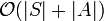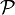F est satisfaisable si et seulement si pour chaque variable propositionnelle $v_i~$ de F, les sommets $v_i~$ et $\lnot v_i$ du graphe 2-SAT sont dans deux composantes fortement connexes distinctes. L'algorithme de Tarjan permet de calculer les composantes fortement connexes d'un graphe orienté en $\mathcal{O}(|S|+|A|)$ , donc 2-SAT est bien de classe $\mathcal{P}$ .

Un autre résultat intéressant, obtenu par Papadimitriou en 1994, concerne la complexité en termes d'espace du problème 2-SAT. Celui-ci est complet pour la classe de complexité NL.

Algorithmes de SAT

La plus évidente des méthodes pour résoudre un problème SAT est de parcourir la table de vérité du problème, mais la complexité est alors exponentielle par rapport au nombre de variables.

Méthode systématique

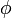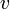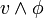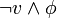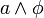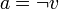Pour prouver la satisfaisabilité du CNF $\phi\$ , il suffit de choisir une variable $v~$ et de prouver récursivement la satisfaisabilité de $v \land \phi$ ou $\neg v \land \phi$ . La procédure est plus facile récursivement puisque $a \land \phi$ avec $a = v\$ ou $a = \neg v$ peut souvent se simplifier. L'appel récursif construit ainsi un arbre binaire de recherche.

Généralement, il existe à chaque nœud des clauses unitaires (la CNF est de la forme 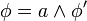$\phi = a \land \phi'$ ), qui permettent de réduire fortement l'espace de recherche.

Exemple

Considérons la CNF :

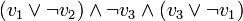$(v_1 \lor \neg v_2) \land \neg v_3 \land (v_3 \lor \neg v_1)$ .

La deuxième clause ( 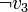$\neg v_3$ ) est unitaire et permet d'obtenir immédiatement

v 3 = f a u x

. On peut remplacer les valeurs de

v 3

dans ce CNF. Cela donne :

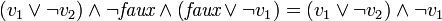$(v_1 \lor \neg v_2) \land \neg \textit{faux} \land (\textit{faux} \lor \neg v_1) = (v_1 \lor \neg v_2) \land \neg v_1$ .

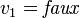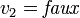À nouveau, on a une clause unitaire, et on obtient $v_1 = \textit{faux}~$ . Puis, par propagation, on obtient $v_2 = \textit{faux}~$ .

Dans cet exemple, on a trouvé les valeurs des trois variables sans même développer l'arbre de recherche. De manière générale, on peut réduire fortement l'espace de recherche. D'autre part, si une variable 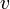$v\$ apparaît toujours positivement dans la CNF 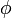$\phi\$ , alors on peut poser 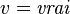$v = \textit{vrai}\$ puisque 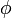$\phi\$ est satisfaisable si et seulement si 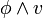$\phi \land v$ est satisfaisable (et de même si la variable apparaît négativement). Ainsi, dans l'exemple précédent, 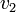$v_2\$ n'apparaît que négativement et l'assignation 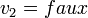$v_2 = faux\$ peut être effectuée. Remarquons que cette affectation permet d'accélérer la découverte d'une solution mais que des solutions pourraient exister en effectuant l'assignation contraire. L'algorithme DPLL (Davis, Putnam^[5], Davis, Logemann, Loveland^[6]) se base sur ces idées.

Le choix de la variable 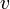$v\$ à développer est très important pour les performances des algorithmes SAT. On choisit généralement les variables qui apparaissent le plus souvent, si possible dans des clauses de taille 2.

Apprentissage de clauses

Le principe de l'apprentissage de clauses est le suivant : lorsqu'un conflit apparaît lors de la recherche, c'est-à-dire lorsque une assignation partielle est démontrée non cohérente avec l'ensemble des clauses, on peut isoler un sous-ensemble de ces assignations et un sous-ensemble de ces clauses, qui sont responsables du conflit (les assignations ne sont pas cohérentes avec les clauses). À partir de ces assignations, il est possible de construire (d'apprendre) une clause qui est impliquée par les clauses. Cette nouvelle clause est ajoutée au CNF. Les assignations pertinentes sont déterminées par un graphe de dépendance entre les clauses et les assignations. Les clauses apprises permettent de ne pas refaire plusieurs fois les mêmes erreurs dans l'arbre de recherche.

Exemple: Considérons que l'assignation ${v 1 = v r a i, v 2 = f a u x, v 3 = f a u x, v 4 = v r a i, v 5 = f a u x}$ mène à un conflit. S'il est démontré que les variables ${v 1, v 4, v 5}$ sont responsables de ce conflit, alors la clause 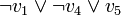$\neg v_1 \lor \neg v_4 \lor v_5$ est impliquée et il est possible de l'ajouter dans la liste des clauses. Si par la suite, la recherche conduit à l'assignation ${v 1 = v r a i, v 2 = v r a i, v 5 = f a u x, v 12 = f a u x}$ , la variable $v 4$ peut être immédiatement assignée à $f a u x$ grâce à la clause apprise.

Approches prospectives

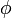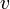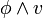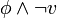L'approche prospective consiste à prospecter l'arbre de recherche pour découvrir des assignations certaines. Ainsi, étant donné un CNF $\phi\$ , étant donnée une variable non instanciée $v\$ , on prospecte les CNFs $\phi \land v$ et $\phi \land \neg v$ . Si les deux CNFs conduisent à l'instanciation de la même variable 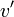$v'\$ avec la même valeur, alors l'instanciation peut se faire dès la CNF $\phi\$ .

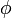Exemple: Considérons la CNF 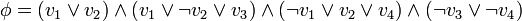$\phi = (v_1 \lor v_2) \land (v_1 \lor \neg v_2 \lor v_3) \land (\neg v_1 \lor v_2 \lor v_4) \land (\neg v_3 \lor \neg v_4)$ . Nous nous intéressons ici à la variable 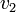$v_2\$ et prospectons la variable 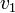$v_1\$ .; Considérons l'assignation 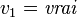$v_1 = \textit{vrai}\$ . On obtient 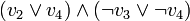$(v_2 \lor v_4) \land (\neg v_3 \lor \neg v_4)$ et donc l'assignation 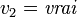$v_2 = \textit{vrai}\$ (puisque cette variable apparaît uniquement positivement).; Considérons l'assignation 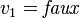$v_1 = \textit{faux}\$ . On obtient 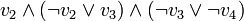$v_2 \land (\neg v_2 \lor v_3) \land (\neg v_3 \lor \neg v_4)$ et donc l'assignation 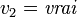$v_2 = \textit{vrai}\$ par clause unitaire.; Dans tous les cas, on obtient 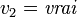$v_2 = \textit{vrai}\$ et il est donc possible d'effectuer cette assignation dès la CNF $\phi\$ .

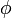Rappelons que la complexité du problème SAT vient de la taille exponentielle de l'arbre de recherche par rapport au nombre de variables. La prospection permet de réduire fortement ce nombre de variables dès la racine (ou à n'importe quel nœud de l'arbre) avec une complexité supplémentaire relativement faible eu égard à la diminution de l'arbre de recherche.

Recherche locale

Partant d'une assignation de toutes les variables, on cherche à modifier certaines valuations de façon à réduire le nombre de clauses non satisfaites. Cet algorithme souffre de plusieurs défauts : il peut tomber dans des minima locaux et il est incapable de prouver la non satisfaisabilité, mais il s'avère très efficace dans les problèmes non structurés (c'est-à-dire souvent les problèmes générés aléatoirement). En cas d'échec après un temps long, il est possible de choisir une nouvelle assignation aléatoire pour éviter les minima locaux.

Principales implémentations

zChaff (Moskewicz, Madigan, Zhao, Zhang 2001)
Siege (Ryan 2003)
MiniSAT (Eén et Sörensson)

Applications

Il est possible de traduire certains problèmes d'intelligence artificielle et d'utiliser les algorithmes SAT pour résoudre efficacement ces problèmes.

Diagnostic

Le diagnostic de systèmes statiques consiste à déterminer si un système a un comportement défectueux étant donnée l'observation des entrées et sorties du système. Le modèle du système peut être traduit en un ensemble de contraintes (disjonctions) : pour chaque composant $c$ du système, une variable $A b (c)$ est créée qui est évaluée à vraie si le composant a un comportement anormal (Abnormal). Les observations peuvent être également traduites par un ensemble de disjonctions. L'assignation trouvée par l'algorithme de satisfaisabilité est un diagnostic.

Planification classique

Le problème de planification classique consiste à trouver une séquence d'actions menant d'un état du système à un ensemble d'états. Étant donnée une longueur maximale du plan $n$ et un ensemble $V$ de variables d'état booléennes permettant de décrire l'état du système, on crée les variables propositionelles $v i$ pour tout 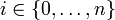$i \in \{0,\dots,n\}$ et toute variable 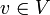$v \in V$ . La variable $v i$ est vraie si la variable d'état est vraie après l'action numéro $i$ . On crée également les variables $a i$ pour tout 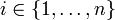$i \in \{1,\dots,n\}$ et toute action $a$ . La variable $a i$ est vraie si l'action numéro $i$ est $a$ . Il est alors possible de transformer le modèle du système en un ensemble de clauses. Par exemple, si l'action $a$ fait passer la variable $v 1$ à vrai lorsque celle-ci est fausse, alors la CNF contiendra une clause 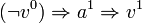$(\neg v^0) \Rightarrow a^1 \Rightarrow v^1$ (ce qui est traduit par la clause 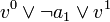$v^0 \lor \neg a_1 \lor v^1$ ). L'assignation trouvée par l'algorithme de satisfaisabilité peut être immédiatement traduite en plan.

La planification classique par SAT est très efficace si on connaît la longueur $n$ du plan. Si cette valeur n'est pas connue, on peut chercher des plans pour une valeur incrémentale, ce qui est parfois coûteux (notamment parce que la CNF est non satisfaisable jusqu'à $n - 1$ ).

Model checking

Une approche semblable a été utilisée pour le model checking (vérification de propriétés d'un modèle). La principale différence est que le model checking s'applique à des trajectoires de longueur infinie contrairement à la planification. Cependant, si l'espace d'états du système est fini, toute trajectoire infinie boucle à un certain point et on peut borner la taille des trajectoires qu'il est nécessaire de vérifier. Le bounded model checking tire parti de cette propriété pour transformer le problème de model checking en un certain nombre de problèmes de satisfaisabilité.

Voir aussi

Problème 3-SAT

Bibliographie

R. Cori et D. Lascar, Logique mathématique, Dunod, 2003, ISBN 2-10-005452-X
J.-M. Alliot, T. Schiex, P.Brisset et F. Garcia, Intelligence artificielle & informatique théorique, Cépaduès, 2002, ISBN 2-85428-578-6
L. Sais, Problème SAT : Progrès et Défis, 2008

Notes

↑ Une valuation sur P est une application de P dans l'ensemble {0,1}, avec P inclus dans l'ensemble des variables propositionnelles.
↑ http://www.cnrtl.fr/lexicographie/satisfaisable?
↑ Cela ne modifie pas la nature du problème, notamment par restriction. En effet, « toute formule du calcul propositionnel est logiquement équivalente à au moins une formule sous forme normale conjonctive et à au moins une formule sous forme normale disjonctive ».
↑ (en) Bengt Aspvall, Michael F. Plass, et Robert E. Tarjan, « A linear-time algorithm for testing the truth of certain quantified boolean formulas », dans Information Processing Letters, 8, p. 121-123 (1979), [lire en ligne]
↑ (en) Martin Davis et Hillary Putnam, « A Computing Procedure for Quantification Theory » , dans Communications of the ACM, 7, p. 201-215 (1960) [lire en ligne]
↑ (en) Martin Davis, George Logemann et Donald Loveland, « A machine Program for Theorem Proving », dans Communications of the ACM, 5, p. 394-397 (1962), [lire en ligne]

Ce document provient de « Probl%C3%A8me SAT ».

Catégories : Algorithmique | Intelligence artificielle | Problème NP-complet

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article SAT (problème) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Probleme SAT — Problème SAT On nomme problème SAT un problème de décision visant à savoir s il existe une solution à une série d équations logiques données. En termes plus précis : une valuation sur un ensemble de variables propositionnelles[1] telle qu… … Wikipédia en Français
Problème 3SAT — Problème 3 SAT Le problème 3 SAT est un cas particulier du problème SAT quand la taille des clauses est exactement de 3. C est l un des 21 problèmes NP complets de Karp. Un exemple d instance de ce problème : E a 4 clauses, 5 littéraux v1,v2 … Wikipédia en Français
SAT — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. {{{image}}} Sigles d une seule lettre Sigles de deux lettres > Sigles de trois lettres … Wikipédia en Français
Sat — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. {{{image}}} Sigles d une seule lettre Sigles de deux lettres > Sigles de trois lettres … Wikipédia en Français
Problème SAT — On nomme problème SAT un problème de décision visant à savoir s il existe une solution à une série d équations logiques données. En termes plus précis : une évaluation sur un ensemble de variables propositionnelles[1] telle qu une formule… … Wikipédia en Français
Problème NP-complet — En théorie de la complexité, un problème NP complet est un problème de décision vérifiant les propriétés suivantes : Il est possible de vérifier une solution efficacement (en temps polynomial) ; la classe des problèmes vérifiant cette… … Wikipédia en Français
Problème 3-SAT — Le problème 3 SAT est un cas particulier du problème SAT quand la taille des clauses est exactement de 3. C est l un des 21 problèmes NP complets de Karp. Un exemple d instance de ce problème : E a 4 clauses, 5 littéraux v1,v2,v3,v4,v5 et… … Wikipédia en Français
SAT-Problem — Das Erfüllbarkeitsproblem der Aussagenlogik (SAT, von engl. satisfiability) ist ein Entscheidungsproblem. Es fragt, ob eine aussagenlogische Formel erfüllbar ist. Anwendungen finden sich unter anderem in der Komplexitätstheorie, Verifikation und… … Deutsch Wikipedia
Problème P = NP — En mathématiques, et plus précisément en informatique théorique, la relation entre la classe des problèmes de complexité P et la classe des problèmes de complexité NP est un problème non résolu, et est considéré par de nombreux chercheurs comme… … Wikipédia en Français
Sat (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sat est le nom de : Sat, un rappeur français, membre de la Fonky Family. Problème SAT, un problème de décision d une grande importance en théorie de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

SAT (problème)

Problème SAT

Sommaire

Définitions

Clause et forme clausale

Le problème SAT

Complexité et restrictions

NP-complétude

Le problème 2-SAT

Algorithmes de SAT

Méthode systématique

Apprentissage de clauses

Approches prospectives

Recherche locale

Principales implémentations

Applications

Diagnostic

Planification classique

Model checking

Voir aussi

Bibliographie

Notes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

SAT (problème)

Problème SAT

Sommaire

Définitions

Clause et forme clausale

Le problème SAT

Complexité et restrictions

NP-complétude

Le problème 2-SAT

Algorithmes de SAT

Méthode systématique

Apprentissage de clauses

Approches prospectives

Recherche locale

Principales implémentations

Applications

Diagnostic

Planification classique

Model checking

Voir aussi

Bibliographie

Notes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link