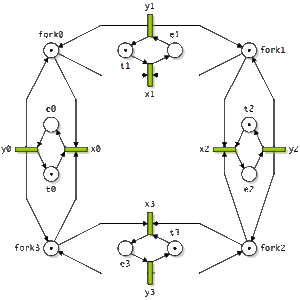
Réseau de Petri

Réseau de Petri
Page d'aide sur l'homonymie Pour les articles homonymes, voir Réseau.
Exemple d'un réseau de Petri Place-Transition, composé de :
  • deux places, les cercles
  • trois transitions, les traits noirs
  • quatre arcs, les flèches
  • deux jetons, les points noirs qui circulent de gauche à droite

Un réseau de Petri (en français on prononce [petʁi̩] ) est un modèle mathématique servant à représenter divers systèmes (informatiques, industriels,…) travaillant sur des variables discrètes.

Sommaire

Histoire

Le problème du diner des philosophe modélisé en Réseau de Petri

Les réseaux de Petri sont apparus en 1962, dans la thèse de doctorat de Carl Adam Petri.

Définition

Un réseau de Petri est un 6-uplet (S,T,F,M_0,W,K)\,, où (cf. Desel et Juhás[1])

  • S définit une ou plusieurs places.
  • T définit une ou plusieurs transitions.
  • F définit un ou plusieurs arcs (flèches).

Un arc ne peut pas être connecté entre 2 places ou 2 transitions ; plus formellement : F \subseteq (S \times T) \cup (T \times S).

  • M_0 : S \to \mathbb{N} appelé marquage initial, où, pour chaque place s \in S, il y a n \in \mathbb{N} jetons.
  • W : F \to \mathbb{N^+} appelé ensemble d'arcs primaires , assignant à chaque arc f \in F un entier positif n \in \mathbb{N^+} qui indique combien de jetons sont consommés depuis une place vers une transition, ou sinon, combien de jetons sont produis par une transition et arrivent pour chaque place.
  • K : S \to \mathbb{N^+} appelé limite de capacité, faisant correspondre à chaque place s \in S un nombre positif n \in \mathbb{N^+} représentant le nombre maximum de jetons qui peuvent occuper une place.

De nombreuses définitions formelles existent. Cette définition concerne un réseau place-transition (ou P-T). D'autres définitions n'incluent pas la notion d'arc primaire ou la limite de capacité.

Représentation

Detailed petri net.png

Un réseau de Petri se représente par un graphe biparti (composé de deux types de nœuds et dont aucun arc ne relie deux nœuds de même type) orienté (composé d'arc(s) ayant un sens) reliant des places et des transitions (les nœuds). Deux places ne peuvent pas être reliées entre elles, ni deux transitions. Les places peuvent contenir des jetons, représentant généralement des ressources disponibles.

La distribution des jetons dans les places est appelée le marquage du réseau de Petri.

Les entrées d'une transition sont les places desquelles part une flèche pointant vers cette transition, et les sorties d'une transition sont les places pointées par une flèche ayant pour origine cette transition.

Représentation matricielle

La définition matricielle introduit les matrices PRE \in \mathcal{M}_{mn} et POST \in \mathcal{M}_{mn}.

  • PREpt = W(p,t)
  • POSTpt = W(t,p)

Ces matrices de même dimension représentent en ligne les places, et en colonne les transitions. PRE contient les valuations des arcs qui vont des places vers les transitions, POST concerne les arcs des transitions vers les places. Une valeur nulle dans une des matrices indique l'inexistence d'un arc dans un sens ou dans l'autre.

La matrice d'incidence C est définie par C = POST − PRE. Étant donnée une transition t, Cpt est le nombre de jetons qui seront ajoutés (ou retirés si le nombre est négatif) à la place p si la transition t est franchie.

Dynamique d'exécution

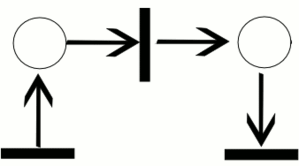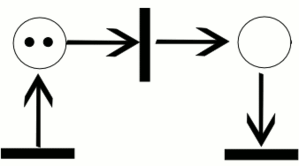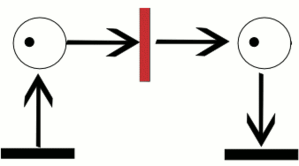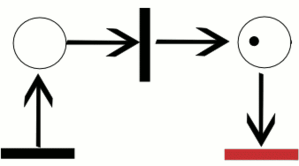
Un réseau de Petri évolue lorsqu'on exécute une transition : des jetons sont retirés dans les places en entrée de cette transition et des jetons sont déposés dans les places en sortie de cette transition.

L'exécution d'une transition (pour un réseau de base ou un réseau coloré) est une opération indivisible qui est déterminée par la présence du jeton sur la place d'entrée.

L'exécution d'un réseau de Petri n'est pas déterministe, car il peut y avoir plusieurs possibilités d'évolution à un instant donné.

Si chaque transition dans un réseau de Petri a exactement une entrée et une sortie alors ce réseau est un automate fini.

Franchissement d'une transition

Le fait que la transition t est franchissable à partir du marquage M se note M \stackrel{t}{\rightarrow}

On dit qu'une transition t est franchissable, si chaque place p en entrée contient un nombre de jetons supérieur ou égal à la valuation de l'arc qui la relie à la transition t. C'est-à-dire :

M \geq PRE_t

Note : PREt est la t-ième colonne de PRE.

Le franchissement d'une transition permet d'atteindre un nouveau marquage M' à partir de M: M \stackrel{t}{\rightarrow} M' :

M' = M + Ct

Séquence de transitions

Une séquence de transitions est une séquence formée sur l'alphabet des transitions (voir Théorie des langages). Elle décrit une suite de transitions à activer.

On dit qu'une séquence de transitions σ = σ't est franchissable à partir du marquage M si:

  • σ' est franchissable à partir de M et M \stackrel{\sigma '}{\rightarrow} M'
  • t est franchissable à partir de M', M' \stackrel{t}{\rightarrow}

A une séquence de transitions σ, on associe un vecteur commutatif \stackrel{\rightarrow}{\sigma} = (\alpha_1, ... , \alpha_m) (m est le nombre de transitions). αi est le nombre d'occurrences de la transitions i dans σ.


Exemple: Soit un réseau avec les transitions T = {t1,t2,t3}. σ = t2t1t3t1, le vecteur commutatif correspondant est \stackrel{\rightarrow}{\sigma} = (2, 1 ,1) (vecteur colonne)

Si la séquence σ est franchissable à partir du marquage M, alors on peut calculer le marquage M' obtenu par \sigma \stackrel{t}{\rightarrow}:

M' = M + C . \stackrel{\rightarrow}{\sigma}

Représentation graphique

Graphe de marquage

Le graphe des marquages d'un réseau (R,M0) est un graphe orienté dont les noeuds sont les marquages de A(R,M0), et chaque arc relie un marquage à un autre qui est immédiatement accessible par une transition : si M_0 \stackrel{t}{\rightarrow} M_1, un arc est tracé de M0 à M1 et il est marqué avec t.

Ce type de graphe donne une vue simple de l'évolution d'un réseau, néanmoins le graphe des marquages n'est pertinent que pour les réseaux bornés[2] : un réseau non borné a une infinité de marquages et ne pourrait être représenté.

L'algorithme de construction du graphe se définit récursivement, partant de l'état initial, on détermine de proche en proche les marquages accessibles.

  • S est l'ensemble des noeuds du graphe, il est initialisé à M0
  • En entrée, l'algorithme prend un marquage M
Pour toute transition t faire
 Si M \stackrel{t}{\rightarrow} M_1 Alors
   Si M_1\notin S Alors
     S \leftarrow S \bigcup \{M_1\}
     Créer le sommet M1
   Fin Si
   Créer l'arc (M,M1)
   Appeler l'algorithme avec M1
 Fin Si
Fin Pour
Reachability graph for petri net.png

Graphe de couverture

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Extensions

Un réseau de Petri de haut niveau est un réseau coloré et hiérarchique.

Couleur

Pour un réseau de Petri de base, on ne distingue pas les différents jetons. Dans un réseau de Petri coloré, on associe une valeur à chaque jeton.

Pour plusieurs outils associés aux réseaux de Petri colorés, les valeurs des jetons sont typées, et peuvent être testées et/ou manipulées avec un langage fonctionnel.

Hiérarchie

Une autre extension du réseau de Petri est la hiérarchie (ou récursivité) : des éléments du réseau de Petri sont eux-mêmes composés d'un réseau de Petri.

Stochastique

Les réseaux de Petri Stochastiques ajoutent de l'indéterminisme et des probabilités de tir.

Notes et références

  1. ↑ Desel, Jörg and Juhás, Gabriel « What Is a Petri Net? Informal Answers for the Informed Reader », Hartmut Ehrig et al. (Eds.): Unifying Petri Nets, LNCS 2128, pp. 1-25, 2001. [1]
  2. ↑ réseau dont toutes les places atteignables ont un nombre fini de jetons

Bibliographie

Outre les références présentées dans l'article en version anglaise, le lecteur francophone pourra consulter :

  • René David et Hassane Alla, Du Grafcet aux réseaux de Petri, Paris, Hermès, 1992, 2ee éd. (ISBN 2-86601-325-5).
    à noter l'ouvrage en anglais traitant plus spécialement des extensions temporelles et continues: René David et Hassane Alla, Discrete, Continuous, and Hybrid Petri Nets, Berlin, Springer-Verlag, 2005 (ISBN 3-540-22480-7) 
     
  • Michel Diaz, Vérification et mise en œuvre des réseaux de Petri : ouvrage collectif sous la direction de Michel Diaz, Hermes Science Publications, coll. « Traité IC2 / Informatique et systèmes d'information » (ISBN 2746204452) 
  • M. Combacau et P. Esteban, Commandes à Réseaux de Petri, coll. « Techniques de l'Ingénieur » [lire en ligne] 
  • PetriParc : Simulateur de Réseaux de Petri sur www.univ-valenciennes.fr/GDR-MACS.
  • Groupe francophone de recherche sur les réseaux de Petri sur lagis.ec-lille.fr.

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Réseau de Petri de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Reseau de Petri — Réseau de Petri Pour les articles homonymes, voir Réseau. Exemple d un réseau de Petri Place Transition, composé de : deux places, les cercles trois transitions, les traits noirs quatre arcs, les flèches deux je …   Wikipédia en Français

  • Réseau de petri — Pour les articles homonymes, voir Réseau. Exemple d un réseau de Petri Place Transition, composé de : deux places, les cercles trois transitions, les traits noirs quatre arcs, les flèches deux je …   Wikipédia en Français

  • réseau de Petri — Petri tinklas statusas T sritis automatika atitikmenys: angl. Petri net vok. Petri Netz, n rus. сеть Петри, f pranc. réseau de Petri, m ryšiai: sinonimas – Petri tinklas …   Automatikos terminų žodynas

  • réseau de Pétri — ● loc. m. ►SPECIF Voir Pétri (réseau de) …   Dictionnaire d'informatique francophone

  • Reseau — Réseau Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Petri net — Petri tinklas statusas T sritis automatika atitikmenys: angl. Petri net vok. Petri Netz, n rus. сеть Петри, f pranc. réseau de Petri, m ryšiai: sinonimas – Petri tinklas …   Automatikos terminų žodynas

  • Petri tinklas — statusas T sritis automatika atitikmenys: angl. Petri net vok. Petri Netz, n rus. сеть Петри, f pranc. réseau de Petri, m ryšiai: sinonimas – Petri tinklas …   Automatikos terminų žodynas

  • Petri-Netz — Petri tinklas statusas T sritis automatika atitikmenys: angl. Petri net vok. Petri Netz, n rus. сеть Петри, f pranc. réseau de Petri, m ryšiai: sinonimas – Petri tinklas …   Automatikos terminų žodynas

  • Petri — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La boîte de Petri, utilisée en biologie comme milieu de culture, a été créée par Julius Richard Petri. Réseau de Petri désigne un modèle mathématique créé …   Wikipédia en Français

  • Réseau — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Réseau », sur le Wiktionnaire (dictionnaire universel) Un réseau est un ensemble de nœuds (ou pôles)… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”