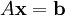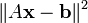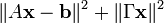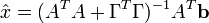Régression d'arête

La régularisation Tychonoff est la méthode de régularisation la plus utilisée pour la résolution de problèmes qui ne sont pas bien posés ainsi que pour les problèmes inverses. Elle a été imaginée par le mathématicien russe Andreï Nikolaïevitch Tikhonov. En statistique, la méthode est également connue sous le nom de régression d'arête (ridge regression). Elle est connexe à l'algorithme de Levenberg-Marquardt pour la résolution de problèmes non-linéaires de moindres carrés.

Sommaire 1 Développement 1.1 Problème 1.2 Régularisation 1.3 Solution 2 Notes et références 3 Voir aussi 3.1 Articles connexes 3.2 Sources 3.3 Liens externes

Développement

Problème

L'approche classique pour résoudre un système d'équations linéaires surdéterminées exprimées par

est connue comme la méthode des moindres carrés et consiste à minimiser le résidu

où est la norme euclidienne. Cependant, la matrice A peut-être mal conditionnée ou non inversible, conduisant à un grand nombre de solutions.

Régularisation

Dans le but de privilégier une solution particulière dotée de propriétés qui semblent pertinentes, un terme de régularisation est introduit dans la minimisation :

Γ, la « matrice de Tikhonov » doit être judicieusement choisie pour le problème considéré. x est le vecteur que l'on cherche à exprimer. x est souvent une approximation discrétisée d'une fonction continue. Dans de nombreux cas, la matrice Γ est la Matrice identité Γ = I, ce qui favorise les solutions dont les normes sont petites. Dans d'autres cas des opérateurs passe-haut, par exemple un Opérateur de différence ou un opérateur de Fourier pondéré peut être utilisé pour éliminer les variations rapides de la fonction lorsque l'on a de bonnes raisons de croire que le vecteur x est l'approximation d'une fonction continue.

Cette régularisation améliore le conditionnement du problème, permettant ainsi de trouver une solution numérique.

Solution

Une solution numérique que l'on va appeler 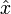est donnée par:

L'effet de la régularisation dépend du choix de la matrice Γ. Lorsque Γ = 0, on en revient au cas de la solution, non régularisée, des moindres carrés, pourvu que (A^TA)⁻¹ existe.

Notes et références

Voir aussi

Articles connexes

Sources

• Dans sa version du 15 août 2008, cet article est, en gros, une traduction de l'article de la wikipédia anglaise qui donne la bibliographie suivante:
• Tikhonov AN, 1943, On the stability of inverse problems, Dokl. Akad. Nauk SSSR, 39, No. 5, 195-198
• Tikhonov AN, 1963, Solution of incorrectly formulated problems and the regularization method, Soviet Math Dokl 4, 1035-1038 English translation of Dokl Akad Nauk SSSR 151, 1963, 501-504
• Tikhonov AN and Arsenin VA, 1977, Solution of Ill-posed Problems, Winston & Sons, Washington, ISBN 0-470-99124-0.
• Hansen, P.C., 1998, Rank-deficient and Discrete ill-posed problems, SIAM
• Hoerl AE, 1962, Application of ridge analysis to regression problems, Chemical Engineering Progress, 58, 54-59.
• Foster M, 1961, An application of the Wiener-Kolmogorov smoothing theory to matrix inversion, J. SIAM, 9, 387-392
• Phillips DL, 1962, A technique for the numerical solution of certain integral equations of the first kind, J Assoc Comput Mach, 9, 84-97
• Tarantola A, 2004, Inverse Problem Theory (free PDF version), Society for Industrial and Applied Mathematics, ISBN 0-89871-572-5
• Wahba, G, 1990, spline Models for Observational Data, SIAM

Liens externes

• Portail des mathématiques