Regularisation (physique)

Regularisation (physique)

Régularisation (physique)

En physique théorique, la régularisation est une procédure ad-hoc qui consiste à modifier une grandeur physique qui présente une singularité afin de la rendre régulière. La régularisation est par exemple abondamment utilisée en théorie quantique des champs en relation avec la procédure de renormalisation, ainsi qu'en relativité générale pour le calcul du problème à deux corps en paramétrisation post-newtonienne.

Sommaire

Exemple élémentaire

Le potentiel newtonien en coordonnées sphériques s'écrit :

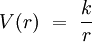
V(r) \ = \ \frac{k}{r}

où k est une constante. Cette expression présente une singularité à l'origine : elle devient en effet infinie en r = 0. On peut la régulariser en introduisant une famille à un paramètre :

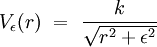
V_{\epsilon}(r) \ = \ \frac{k}{\sqrt{r^2 + \epsilon^2}}

Cette expression reste bien définie en r = 0, car pour tout ε > 0, on a :

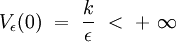
V_{\epsilon}(0) \ = \ \frac{k}{\epsilon} \ < \ + \ \infty

Régularisations en théorie quantique des champs

Les calculs de processus de diffusion en théorie quantique des champs perturbative font apparaitre des intégrales divergentes dès l'ordre d'une boucle. Pour donner un sens à ces intégrales, plusieurs méthodes sont utilisées.

Régularisation dimensionnelle

Initialement, l'espace-temps physique réel possède une dimension d = 4. La régularisation dimensionnelle consiste en un prolongement analytique de l'intégrale divergente pour des dimensions d'espace-temps d complexes, la fonction obtenue étant méromorphe. Il est alors possible d'étudier la nature de la singularité en d = 4 afin de procéder à une renormalisation par soustraction du terme divergent. La méthode, qui respecte l'unitarité, la causalité et l'invariance de jauge, a été introduite en 1972 par t'Hooft & Veltman[1], Bollini & Giambiagi[2], et Ashmore[3].


Considérons par exemple l'intégrale typique suivante, correpondante à la somme sur la quadri-impulsion p dans une boucle[4] :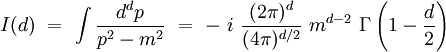

I(d) \ = \ \int \frac{d^dp}{p^2 - m^2} \ = \ - \ i \ \frac{(2 \pi)^d}{(4 \pi)^{d/2}} \ m^{d-2} \ \Gamma \left( 1 - \frac{d}{2} \right)

où Γ(z) est la fonction gamma d'Euler. Pour étudier la singularité en d = 4, on pose : ε = 4 − d et on fait un développement asymptotique en zéro :

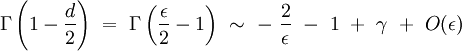
\Gamma \left( 1 - \frac{d}{2} \right) \ = \ \Gamma \left( \frac{\epsilon}{2} - 1 \right) \ \sim \ - \ \frac{2}{\epsilon} \ - \ 1 \ + \ \gamma \ + \ O(\epsilon)

où γ est la constante d'Euler-Mascheroni. On en déduit que l'intégrale I(d) présente un pôle simple en d = 4 :

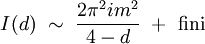
I(d) \ \sim \ \frac{2 \pi^2 i m^2}{4-d} \ + \ \mathrm{fini}

Régularisation de Pauli-Villars

Cette méthode consiste à rajouter des particules fictives de masse M à la théorie initiale ; on étudie alors la limite M tendant vers l'infini. Elle a été publiée[5] en 1949 par Pauli and Villars, basée sur des travaux antérieurs de Feynman, Stueckelberg et Rivier.

Régularisation zêta

Article détaillé : Régularisation zêta.

Notes et références

  1. ↑ Gerard t'Hooft & Martinus Veltman ; Regularization & renormalization of gauge fields, Nuclear Physics B 44 (1972), 189-213.
  2. ↑ CG Bollini & JJ Giambiagi ; Lowest order "divergent" graphs in n-dimmensional space, Physics Letter B 40 (1972), 566-568.
  3. ↑ JF Ashmore ; A method of gauge invariant regularization, Nuovo Cimento Letters 4 (1972), 289-290.
  4. ↑ Cet exemple est tiré d'un « modèle-jouet » : la théorie du champ scalaire autointeragissant 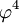\varphi^4. Cette intégrale apparait dans la correction à une boucle du propagateur libre. Les détails du calcul se trouvent e.g. dans : Lewis H Ryder ; Quantum Field Theory, Cambridge University Press (1985), ISBN 0-521-33859-X, paragraphe 9.2, page 349.
  5. ↑ W Pauli & F Villars ; On the Invariant Regularization in Relativistic Quantum Theory, Review of Modern Physics 21 (1949), 434-444.


Voir aussi

Articles connexes

Bibliographie

  • Anthony Zee ; Quantum Field Theory in a Nutshell, Princeton University Press (2003), ISBN 0-691-01019-6.
  • Lewis H Ryder ; Quantum Field Theory (Cambridge University Press, 1985), ISBN 0-521-33859-X.
  • Silvian S. Schweber ; QED and the men who made it: Dyson, Feynman, Schwinger, and Tomonaga, Princeton University Press (1994), ISBN 0-691-03327-7.
  • Gerard t'Hooft ; This week's Citation Classic (16 avril 1984). pdf.


  • Portail de la physique Portail de la physique
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « R%C3%A9gularisation (physique) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Regularisation (physique) de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Régularisation (physique) — En physique théorique, la régularisation est une procédure ad hoc qui consiste à modifier une grandeur physique qui présente une singularité afin de la rendre régulière. La régularisation est par exemple abondamment utilisée en théorie quantique… …   Wikipédia en Français

  • Regularisation zeta — Régularisation zêta La régularisation zêta est une méthode de régularisation des déterminants d opérateurs qui apparaissent lors de calculs d intégrales de chemins en théorie quantique des champs. Sommaire 1 Le cas du Laplacien 2 Fonction zêta… …   Wikipédia en Français

  • Régularisation zeta — Régularisation zêta La régularisation zêta est une méthode de régularisation des déterminants d opérateurs qui apparaissent lors de calculs d intégrales de chemins en théorie quantique des champs. Sommaire 1 Le cas du Laplacien 2 Fonction zêta… …   Wikipédia en Français

  • Regularisation — Régularisation Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En droit, la régularisation est une mise en conformité d un acte juridique ou d un acte de procédure. En physique théorique, la… …   Wikipédia en Français

  • Régularisation zêta — La régularisation zêta est une méthode de régularisation des déterminants d opérateurs qui apparaissent lors de calculs d intégrales de chemins en théorie quantique des champs. Sommaire 1 Le cas du Laplacien 2 Fonction zêta spectrale 2.1 …   Wikipédia en Français

  • Régularisation — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En droit, la régularisation est une mise en conformité d un acte juridique ou d un acte de procédure. En physique théorique, la régularisation est une… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Variable régionalisée — La VR comme phénomène physique : topographie de la ville de Binche …   Wikipédia en Français

  • Renormalisation — Traduction à relire Renormalization → Reno …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”