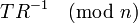Réduction de montgomery

La réduction de Montgomery est un algorithme efficace pour la multiplication en arithmétique modulaire introduite en 1985 par Peter L. Montgomery. Plus concrètement, c'est une méthode pour calculer:

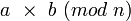
La méthode est surtout efficace lorsque qu'un grand nombre de multiplications modulaires avec un même n doivent être effectuées car le calcul nécessite des étapes de normalisation. Elle est donc particulièrement adaptée au calcul d'Exponentiation modulaire.

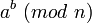
Elle est maintenant très utilisée en cryptologie.

Enoncé formel

Soit n est un nombre entier positif, et soit R et T des entiers tels que R > n, pgcd(n,R) = 1 et 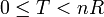. La réduction de Montgomery de T modulo n qui préserve R est défini comme la valeur

R ^{− 1} est l'inverse modulaire de R et mod désigne la congruence sur les entiers. La fonction de réduction peut être décrite à l'aide du pseudo-code suivant:

fonction reduction(T,N,R) {
 
  /* Calcul du nombre de multiples à ajouter pour que */
  /* T + m*N soit divisible par R                     */
  ni = R-ModInverse(N,R);
  m = ((T mod R) * ni) mod R;  
  /* Ajout des multiples et décalage */
  x = (T + m*N) / R;           
  if (x < N)  return x;
  else        return x - N;
 
}

ou ModInverse(N,R) désigne l'inverse modulaire de N (mod R). Si on choisit R = 2^k et que ni peut être pré-calculé alors la fonction ci-dessus se réduit à 2 multiplications (en négligeant le temps pris par les autres opérations moins couteuses).

Multiplication de Montgomery

L'algorithme de la multiplication de Montgomery est très simple. Il suffit à chaque pas (ligne) d'une multiplication classique d'ajouter un multiple de n bien choisi de façon à faire apparaître des 0 dans le résultat. Le modulo n se réduit alors à un simple décalage des digits. Cette opération d'ajout de multiples de n est autorisée puisque l'on travaille modulo n. Un choix de R classique en base 2 consiste à prendre: 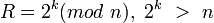et k multiple de 32. L'algorithme calcule 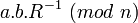. Attention, dans certain cas, l'algorithme retourne un résultat compris entre n et 2n. Il faut alors retrancher n au résultat.

Exemple en base 10

Soit à calculer 234*167 (mod 293), on choisit R=10⁶ (mod 293)=284 pour 6 digits, il suffit de multiplier a ou b par R pour obtenir 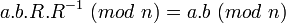. En choisissant a ou b égal à 1, on obtient une réduction modulo n simple. R (ici réduit mod n) étant inférieur à n, la condition a.b<R (non réduit) est suffisante pour éviter un dépassement.

   066456  (234*284)
 x 000167
   ------
1) 465192
  +  1758  (6x293)
   466950
   ------
2) 445431  (398736+466950/10)
  +   879  (3x293)
   446310  
   ------
3) 111087  (66456+446310/10)
  +   293  (1x293)
   111380  
   ------
4)  11138
  +  1172  (4x293)
    12310  
   ------
5)   1231
  +   879  (3x293)
     2110  
   ------
6)    211
  +   879  (3x293)
     1090
   ------
  =   109

On obtient bien le résultat, néanmoins il faut effectuer la normalisation (*284),ce qui coûte une multiplication supplémentaire et un nombre de digits plus grand mais ce procédé peut être adapté en fonction du besoin de façon à minimiser le nombre de multiplications ainsi que le nombre de digits nécessaires. Le calcul du nombre de multiples à ajouter à chaque ligne requiert l'inversion modulaire d'un seul digit, ici le 3 de 293 (voir ci-dessous). A noter, qu'en base 10, n ne peut pas se terminer par 0,2,4,5,6,8. L'utilisation d'une base 2^p est beaucoup plus pratique.

Exemple pour l'étape 1) , On a 3 ^{− 1} = 7 (mod 10), on veut trouver b tel que .

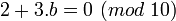       2 + b*3 = 0        (mod 10)
       b*3     = -2       (mod 10) = 8  (mod 10)
       b       = 8 * 3^-1 (mod 10)
       b       = 8 * 7    (mod 10) = 56 (mod 10) = 6