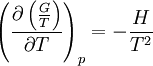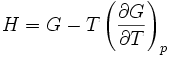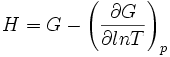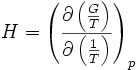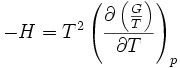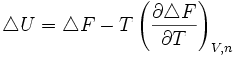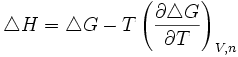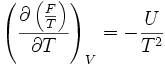Relations d'Helmholtz

Relations d'Helmholtz

Relation de Gibbs-Helmholtz

La relation de Gibbs-Helmholtz (nom donné en l'honneur des physiciens Gibbs et Helmholtz) est donnée par :

\left (\frac{\partial \left ( \frac{G}{T}\right )}{\partial T}\right )_p = -\frac{H}{T^2}

Avec:

On trouve aussi d'autres formulations équivalentes de cette relation :

\qquad H = G - T\left(\frac{\partial G}{\partial T}\right)_p
\qquad H = G - \left(\frac{\partial G}{\partial ln T}\right)_p
H= \left (\frac{\partial \left ( \frac{G}{T}\right )}{\partial \left ( \frac {1}{T} \right )}\right )_p


-H= T^2 \left (\frac{\partial \left ( \frac{G}{T}\right )}{\partial T}\right )_p

Sommaire

Démonstration

Cette relation se montre simplement en partant des relations de Maxwell, et en particulier celle concernant S:

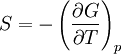
S= -\left(\frac{\partial G}{\partial T}\right)_p
G=H-TS~
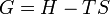
  • avec ce qui précède:
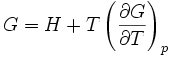
G=H+T\left(\frac{\partial G}{\partial T}\right)_p


  • d'où:
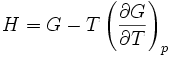
    H=G-T\left(\frac{\partial G}{\partial T}\right)_p


  • en multipliant par 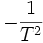-\frac{1}{T^2} la relation précédente:

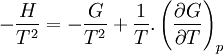
-\frac{H}{T^2}=-\frac{G}{T^2}+\frac{1}{T}.\left(\frac{\partial G}{\partial T}\right)_p


  • on reconnait au 2e terme la dérivée partielle de 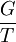\frac{G}{T} par rapport à T, à p constante:


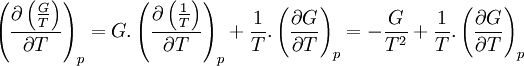
\left(\frac{\partial \left(\frac{G}{T}\right)}{\partial T}\right)_p = G.\left(\frac{\partial \left(\frac{1}{T}\right)}{\partial T}\right)_p + \frac{1}{T}.\left(\frac{\partial G}{\partial T}\right)_p = -\frac{G}{T^2}+\frac{1}{T}.\left(\frac{\partial G}{\partial T}\right)_p


  • on en déduit la relation de relation de Gibbs-Helmholtz:

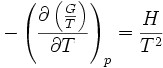
-\left (\frac{\partial \left ( \frac{G}{T}\right )}{\partial T}\right )_p = \frac{H}{T^2}

Autres formulations

On rencontre aussi les relations de Gibbs-Helmholtz sous les formes équivalentes suivantes :

\qquad \triangle U = \triangle F - T\left(\frac{\partial \triangle F}{\partial T}\right)_{V,n}
\qquad \triangle H = \triangle G - T\left(\frac{\partial \triangle G}{\partial T}\right)_{V,n}

Notations utilisées dans cet article

Intérêt

Cette relation permet d'accéder facilement à l'enthalpie libre quand on connait les variations de l'enthalpie par rapport à la température à pression constante, et vice-versa. Elle fait partie des relations extrèmement utiles en thermodynamique pour passer d'un fonction d'état à une autre.

Remarque

Une relation analogue existe entre F (l'énergie libre), U (l'énergie interne), et T, même si celle-ci est beaucoup moins utilisée que la précédente:

\left (\frac{\partial \left ( \frac{F}{T}\right )}{\partial T}\right )_V = -\frac{U}{T^2}

Celle-ci se montre de la même manière, en partant de la définition de F (F=U-TS)

et de la relation de Maxwell:

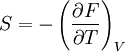
S= -\left(\frac{\partial F}{\partial T}\right)_V

Ces formules font apparaitrent la différence entre les variations d'enthalpie et d'enthalpie libre pour la première formule et la différence entre les variations d'énergie interne et d'énergie libre pour la deuxième formule

  • Portail de la physique Portail de la physique
Ce document provient de « Relation de Gibbs-Helmholtz ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Relations d'Helmholtz de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Helmholtz theorem (classical mechanics) — For other uses, see Helmholtz theorem .The Helmholtz theorem of classical mechanics reads as follows:Let:H(x,p;V)=K(p)+varphi(x;V) be the Hamiltonian of a one dimensional system, where :K=frac{p^2}{2m} is the kinetic energy and :varphi(x;V) is a… …   Wikipedia

  • Relations between heat capacities — The laws of thermodynamics imply the following relations between the heat capacity at constant volume, C {V}, and the heat capacity at constant pressure, C {P}::C {P} C {V}= V Tfrac{alpha^{2{eta {T,:frac{C {P{C {V=frac{eta {T{eta {S,Here alpha …   Wikipedia

  • Maxwell relations — Thermodynamics …   Wikipedia

  • Relation de gibbs-helmholtz — La relation de Gibbs Helmholtz (nom donné en l honneur des physiciens Gibbs et Helmholtz) est donnée par : Avec: H l enthalpie G l enthalpie libre T la température (absolue) On trouve aussi d autres formulations équivalentes de cette… …   Wikipédia en Français

  • Équation de Gibbs-Helmholtz — Relation de Gibbs Helmholtz La relation de Gibbs Helmholtz (nom donné en l honneur des physiciens Gibbs et Helmholtz) est donnée par : Avec: H l enthalpie G l enthalpie libre T la température (absolue) On trouve aussi d autres formulations… …   Wikipédia en Français

  • Onsager reciprocal relations — Thermodynamics …   Wikipedia

  • Relation de Gibbs-Helmholtz — La relation de Gibbs Helmholtz (nom donné en l honneur des physiciens Gibbs et Helmholtz) est donnée par : Avec: H l enthalpie G l enthalpie libre T la température (absolue) On trouve aussi d autres formulations équivalentes de cette… …   Wikipédia en Français

  • Énergie libre de Helmholtz — Énergie libre Potentiels thermodynamiques Énergie interne U(S,V,N) Énergie libre F(T,V,N) = U − TS Enthalpie H(S,p,N) = U + pV …   Wikipédia en Français

  • Generalized Helmholtz theorem — The generalized Helmholtz theorem is the multi dimensional generalization of the Helmholtz theorem which is valid only in one dimension. The generalized Helmholtz theorem reads as follows.Let:mathbf{p}=(p 1,p 2,...,p s), :mathbf{q}=(q 1,q 2,...,q …   Wikipedia

  • Le Meilleur Des Mondes — Pour les articles homonymes, voir Le meilleur des mondes (homonymie). Le Meilleur des mondes Auteur Aldous Huxley Genre Roman …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”