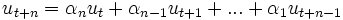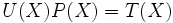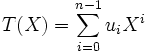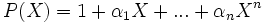Registre a decalage

Registre a decalage

Registre à décalage

En électronique et en informatique, un registre à décalage est un registre de taille fixe dans lequel les bits sont décalés à chaque coup d'horloge (dans le cas d'un système synchrone sur l'horloge).

Un registre à décalage est en général constitué d'un chaînage de bascules synchronisées sur l'horloge, la sortie d'une bascule étant reliée à l'entrée de la suivante. Il se décline en plusieurs variantes :

  • SIPO (Serial In - Parallel Out)
  • SISO (Serial In - Serial Out)
  • PISO (Parallel In - Serial Out)
  • PIPO (Parallel In - Parallel Out)

Les entrées ou sorties en parallèle permettent d'insérer et de récupérer plusieurs bits en même temps. Prenons exemple d'une information de 4 bits (ex: 1001).

  • Parallèle réfère à 4 fils qui renvoient chacun un bit. Donc, le premier fil renvoi "1" en même temps que le deuxième renvoi "0" ainsi de suite.à
  • Série réfère à 1 fil qui envoi "1" suivi de "0" et de "0" et enfin de "1". Le système série prend donc moins de fils mais plus de temps.

Signalons également l'existence de registres à décalage réversibles, càd. de registres où le décalage s'effectue vers la droite ou vers la gauche en fonction du niveau logique appliqué à l'entrée "Sens de décalage".

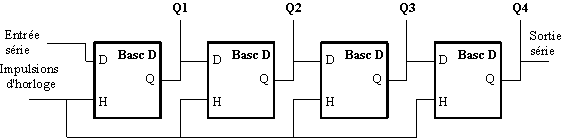Registre à décalage SISO ou SIPO

Sommaire

Exemples d'applications

  • SISO : L'information que l'on veut introduire dans le registre est présentée à l'entrée de la première bascule. Lors d'une impulsion d'horloge, le bit d'information est introduit dans le registre, et tous les autres bits sont décalés. Le bit qui était mémorisé dans la dernière bascule est perdu s'il n'est pas stocké ou réinséré dans la structure d'une manière quelconque. Les registres SISO sont utilisés pour réaliser des lignes à retard numériques. Le délai entre l'entrée de l'information dans le registre et sa sortie dépend du nombre de bascules et de la fréquence d'horloge.
  • PIPO : En décalant tous les bits d'un nombre binaire vers la droite ou vers la gauche, on divise ou on multiplie le nombre par 2. Un registre PIPO peut donc être utilisé pour effectuer des calculs (multiplication ou division par une puissance de 2). Il suffit d'opérer le nombre adéquat de décalages vers la gauche ou la droite entre le moment où l'on introduit les bits dans le registre et le moment où on les récupère.
  • PISO et SIPO : Ces deux types de registres sont utilisés dans les liaisons série ; ils forment la base des UART et des modems. Imaginons que l'on veuille transmettre une information entre deux ordinateurs distants de quelques mètres ou dizaines de mètres. Transmettre l'information sous forme "parallèle" nécessiterait au moins 9 fils (8 pour les 8 bits, un pour la masse), sans compter les fils supplémentaires pour le dialogue entre les ordinateurs. Il est plus simple d'employer un registre PISO pour envoyer les bits constituant chaque octet que l'on désire transmettre en une suite de 8 bits apparaissant l'un après l'autre sur une seule ligne. Au bout de la ligne, un registre SIPO reçoit les bits qui arrivent à la queue-leu-leu et reconstitue des octets qui sont transmis à l'ordinateur de destination.
  • Registres SISO réversibles : Ils permettent par exemple de réaliser ce que l'on appelle des piles LIFO (Last In, First Out) : on charge les bits dans le registre ; puis on inverse le sens du décalage. Les bits apparaissent à la sortie de la première bascule dans l'ordre inverse de leur entrée.

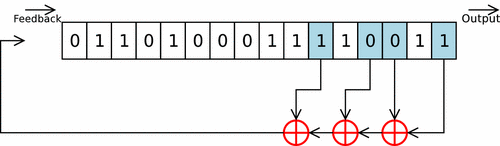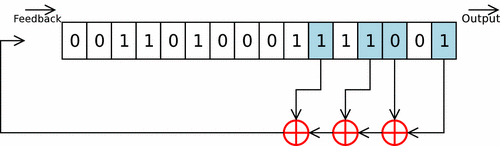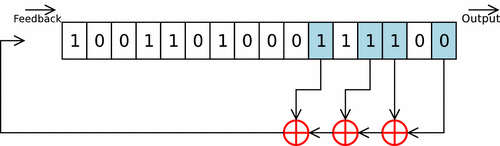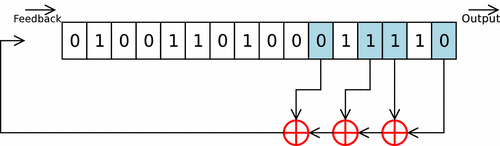
Registre à décalage avec rétroaction linéaire

Il s'agit d'une variante avec une unité logique ou arithmétique (Linear Feedback Shift Register ou LFSR en anglais). Le ou les bit(s) en sortie du registre subissent une série d'opérations et de transformations pour être réinsérés dans le registre. Ce type de registre est utilisé en cryptographie pour les implantations matérielles de certains algorithmes de chiffrement de flot. On les retrouve aussi dans certains microprocesseurs dédiés au traitement de signal (DSP), en particulier pour le filtrage. Ce type de circuit est aussi utilisé lors de la phase de test des circuits intégrés en permettant la génération automatique d'entrées (vecteurs de tests).

Rétroaction basée sur un XOR entre plusieurs bits

Description mathématique

Représentation par les suites

Les suites de bits pouvant être produites par un registre à décalage à rétroaction linéaire sont simples à décrire mathématiquement : ce sont les suites récurrentes linéaires. Autrement dit, on peut obtenir le terme 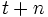t+n~ à partir des termes 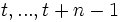t,...,t+n-1~ par une équation linéaire du type

u_{t+n}= \alpha_n u_{t}+\alpha_{n-1} u_{t+1}+...+\alpha_{1} u_{t+n-1}~

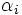où les \alpha_i~ valent 0 ou 1.

Représentation polynômiale

Il est également possible de les décrire en utilisant les séries formelles :

si à une suite 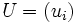U=(u_i)~ on associe la série 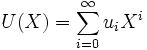U(X)=\sum_{i=0}^{\infty} u_iX^i~ alors l'équation ci-dessus peut se mettre sous la forme suivante :

U(X) P(X)= T(X)~

où

  • T(X)=\sum_{i=0}^{n-1} u_iX^i
  • P(X)=1+\alpha_1 X+ ... +\alpha_n X^n~

Le polynôme 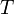T~ correspond à l'initialisation du registre, alors que le polynôme P, appelé polynôme de rétroaction, caractérise le registre.

Périodicité

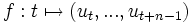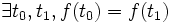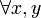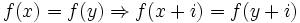Il est facile de voir qu'une suite produite par un tel registre est nécessairement périodique : le nombre de possibilité pour un n-uplet est au plus de 2n, donc f:t\mapsto (u_{t},...,u_{t+n-1}) est surjective, soit \exists t_0,t_1, f(t_0)=f(t_1). Mais, clairement on a \forall x,y et i, f(x)=f(y)\Rightarrow f(x+i)=f(y+i). En prenant i = max(t0 − t1,t1 − t0) on a donc un multiple de la période de la suite.

La période maximale est 2n − 1 car si le n-uplet tout à zéro est atteint, la suite est nécessairement constante égal à zéro. On sait prévoir lorsque cette valeur atteinte, une condition nécessaire et suffisante étant que le polynôme de rétroaction soit primitif -- i.e. est irréductible et tel que, dans l'anneau F2[X] des polynômes à coefficients binaires, le plus petit t tel que ce polynôme divise Xt − 1 est 2n − 1 (c'est le polynôme minimal d'un élément d'ordre multiplicatif 2n − 1 dans le corps à 2n éléments).

Une suite de période maximale est appelée m-sequence dans la terminologie anglo-saxonne.

Notion de complexité linéaire

Tout m-uplet de bits peut être généré par un LFSR. Plus précisément, il existe toujours un LFSR -- i.e. un polynôme de rétroaction ainsi qu'une initialisation -- tel que les m premières sorties de ce LFSR correspondent au m-uplet. Dans le pire des cas on prend un registre de longueur m, le polynôme de rétroaction important peu dans ces conditions.

Ceci donne lieu à la définition de la complexité linéaire d'une suite (finie) comme la longueur minimale d'un LFSR généré cette suite. Comme le prouve la remarque ci-dessus cette complexité est bornée supérieurement par la longueur de la suite.

Cette notion intervient notamment en cryptographie à cause de l'existence de l'algorithme de Berlekamp-Massey.

Registre à décalage et cryptographie

Génération de pseudo-aléatoire

Un problème fondamental en cryptologie est la production de suites de bits «aussi aléatoires que possible». Un exemple évident étant la génération des clefs de chiffrement (symétrique ou asymétrique).

Ce problème se décompose en fait en deux parties : d'une part la génération de bits par des procédés physiques -- mesure de temps entre frappes de touches sur un clavier, déplacement de la souris, ... --, et d'autre part l'expansion d'une courte suite aléatoire de bits en une suite beaucoup plus grande. Dans ce dernier cas, on parle de suite pseudo-aléatoire.

Le chiffrement par masque jetable illustre bien les enjeux. Dans ce chiffrement, le texte chiffré est produit par addition bit à bit (modulo 2) de la clef de chiffrement. Le déchiffrement est également effectué par addition bit à bit de la clef. Le problème est qu'il est alors nécessaire de partager une donnée secrète, à savoir la clef, de la même taille que le message à échanger. C'est très souvent impraticable. Vient alors l'idée d'engendrer la clef à partir d'un procédé déterministe -- il faut pouvoir le faire au chiffrement et au déchiffrement -- utilisant une donnée secrète plus petite. C'est probablement un peu de là l'origine du chiffrement par flot.

Une première possibilité consiste à choisir un LFSR et à utiliser la donnée secrète partagée comme initialisation du registre. Toutefois, l'algorithme de Berlekamp-Massey met vite fin à cette tentative : une connaissance même très partielle de la suite produite permet de retrouver toutes les informations voulues.

Dans la pratique, les LFSRs ne sont donc pas utilisés de manière isolée, mais essentiellement sous la forme des registres combinés ou filtrés.

Algorithme de Berlekamp-Massey

Un LFSR de taille n produisant des suites récurrentes linéaires d'ordre n, la connaissance de n termes consécutifs d'une suite et de l'équation linéaire -- ou bien de manière équivalente le polynôme de rétroaction -- détermine toute la suite.

Si maintenant on ne suppose plus connu le polynôme de rétroaction, que peut-on déduire de l'observation d'une partie de la sortie du LFSR, par exemple les termes 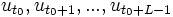u_{t_0},u_{t_0+1},...,u_{t_0+L-1} ? L'algorithme de Berlekamp-Massey répond à cette question de la façon suivante : si L est supérieur où égal à deux fois la taille du plus petit LFSR générant la suite (ui) alors on peut retrouver le polynôme de rétroaction et l'initialisation du registre. En abrégé : tout. On voit ainsi apparaître la complexité linéaire comme le paramètre permettant d'estimer la quantité d'information nécessaire pour recréer une suite sous forme de LFSR.

L'algorithme de Berlekamp-Massey fut introduit en 1969 par James Massey (Massey, J. L. "Shift-Register Synthesis and BCH Decoding." IEEE Trans. Information Th. 15, 122-127, 1969.). C'est une adaptation d'un algorithme, du à Elwyn Berlekamp, de décodage de codes correcteurs -- les codes de Bose-Chaudhuri-Hocquenghem.

Utilisation

  • chiffrement par flot en cryptologie
  • division par une puissance de deux (décalage vers la gauche ou la droite)
  • tampons pour la réception de données (FIFO : first in - first out)
  • compteur, temporisateur

Voir aussi

Wikibooks-logo-fr.png

Wikibooks propose un ouvrage abordant ce sujet : la logique combinatoire.

Wikibooks-logo-fr.png

Wikibooks propose un ouvrage abordant ce sujet : la logique séquentielle.

Liens externes


Crypto key.png Générateurs de nombres pseudo-aléatoires
Modifier
Rapides : Générateur congruentiel linéaire, Mersenne Twister, RANDU
Cryptographiques : Blum Blum Shub, Fortuna, ISAAC, Yarrow
Briques : Congruence sur les entiers, Fonction de hachage, Registre à décalage
Voir aussi le portail de la cryptologie
  • Portail de l’informatique Portail de l’informatique
  • Portail de la cryptologie Portail de la cryptologie
  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
Ce document provient de « Registre %C3%A0 d%C3%A9calage ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Registre a decalage de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Registre à décalage — ● Registre à décalage registre sur lequel on peut effectuer des opérations de décalage …   Encyclopédie Universelle

  • Registre à décalage — Un registre à décalage est un registre, c est à dire un ensemble de bascules synchrones, dont les bascules sont reliées une à une, à l exception de deux bascules qui ne sont pas forcément reliées. A chaque cycle d horloge, le nombre représenté… …   Wikipédia en Français

  • registre à décalage — postūmio registras statusas T sritis automatika atitikmenys: angl. shift register vok. Schieberegister, n rus. сдвиговый регистр, m pranc. registre à décalage, m …   Automatikos terminų žodynas

  • Registre à décalage à rétroaction linéaire — Un registre à décalage à rétroaction linéaire, ou LFSR (acronyme de l anglais linear feedback shift register), est un dispositif électronique ou logiciel qui produit une suite récurrente linéaire, initialement sur le corps fini à 2 élements (0 et …   Wikipédia en Français

  • registre de décalage à couplage de charge — krūvio sąsajos postūmio registras statusas T sritis radioelektronika atitikmenys: angl. charge coupled shift register vok. Ladungskopplungsschieberegister, n rus. сдвиговый регистр на приборах с зарядовой связью, m pranc. registre de décalage à… …   Radioelektronikos terminų žodynas

  • registre à décalage à barillet — ciklinio postūmio registras statusas T sritis automatika atitikmenys: angl. circulating register vok. Ringschieberegister, n; Umlaufregister, n rus. регистр с циркуляцией кода, m; циклический сдвиговый регистр, m pranc. registre à décalage à… …   Automatikos terminų žodynas

  • registre de décalage à chapelet — kopėtėlinio postūmio registras statusas T sritis radioelektronika atitikmenys: angl. bucket brigade shift register vok. Eimerkettenschieberegister, n rus. сдвиговый регистр типа пожарная цепочка , m pranc. registre de décalage à chapelet, m …   Radioelektronikos terminų žodynas

  • décalage — [ dekalaʒ ] n. m. • 1845; de décaler 1 ♦ Le fait de décaler (2o) dans l espace, le temps; écart temporel ou spatial. Décalage des lignes de départ, sur une piste de stade. Un décalage de deux mètres, d une semaine. Spécialt Décalage horaire. Un… …   Encyclopédie Universelle

  • Registre de processeur — Registre (informatique) Pour les articles homonymes, voir Registre. En architecture des ordinateurs, un registre est un emplacement de mémoire interne à un processeur. Les registres se situent au sommet de la hiérarchie mémoire : il s agit… …   Wikipédia en Français

  • Registre (informatique) — Pour les articles homonymes, voir Registre. Un registre est un emplacement de mémoire interne à un processeur. Les registres se situent au sommet de la hiérarchie mémoire : il s agit de la mémoire au meilleur temps d accès, mais dont le coût …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”