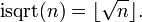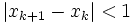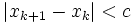Racine carree entiere

Racine carree entiere

Racine carrée entière

En mathématiques et en théorie des nombres, la racine carrée entière (isqrt) d'un nombre entier positif n est l'entier positif m qui est le plus grand entier inférieur ou égal à la racine carrée de n,

\mbox{isqrt}( n ) = \lfloor \sqrt n \rfloor.

Sommaire

Algorithme

Pour calculer 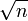\sqrt{n}, et en particulier, isqrt(n), on peut utiliser la méthode de Newton pour l'équation 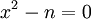x^2-n=0\,, qui nous donne la formule récursive

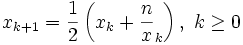{x}_{k+1} = \frac{1}{2}\left(x_k + \frac{ n }{x}_{k}\right), \ k \ge 0.

On peut choisir par exemple 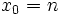x_0=n\, comme condition initiale.

La suite {xk} converge de manière quadratique vers 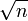\sqrt{n} lorsque 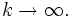k \to \infty. Il peut être démontré (la démonstration n'est pas triviale) que l'on peut stopper dès que

|x_{k+1}-x_k| < 1\,

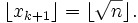
pour que \lfloor x_{k+1} \rfloor=\lfloor \sqrt n \rfloor.

Domaine de calcul

Même si 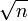\sqrt n est irrationnel pour la plupart des n, la suite {xk} contient seulement des termes rationnels. Ainsi, avec la méthode de Newton, on n'a jamais besoin de quitter le corps des nombres rationnels pour calculer isqrt(n), un résultat qui possède certains avantages théoriques en théorie des nombres.

Le critère d'arrêt

On peut démontrer que c = 1 est le plus grand nombre possible pour lequel le critère d'arrêt

|x_{k+1}-x_k| < c\,

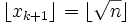pour que \lfloor x_{k+1} \rfloor=\lfloor \sqrt n \rfloor dans l'algorithme ci-dessus.

Puisque les calculs informatiques actuels impliquent des erreurs d'arrondi, on a besoin d'utiliser 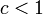c < 1\, dans le critère d'arrêt, c'est-à-dire :

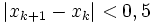|x_{k+1}-x_k| < 0,5\,.

Voir aussi

Ce document provient de « Racine carr%C3%A9e enti%C3%A8re ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Racine carree entiere de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Racine Carrée Entière — En mathématiques et en théorie des nombres, la racine carrée entière (isqrt) d un nombre entier positif n est l entier positif m qui est le plus grand entier inférieur ou égal à la racine carrée de n, Sommaire 1 Algorithme 2 …   Wikipédia en Français

  • Racine carrée entière — En mathématiques et en théorie des nombres, la racine carrée entière (isqrt) d un nombre entier positif n est l entier positif m qui est le plus grand entier inférieur ou égal à la racine carrée de n, Sommaire 1 Algorithme 2 Domaine de calcul …   Wikipédia en Français

  • Racine Carrée De 2 — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine Carrée De Deux — L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine carree de deux — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine carrée de 2 — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

  • Racine carrée — La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x½; dans cette expression, x est appelé le radicande. Une tablette d argile datée du XVIIIe siècle av. J.‑C. montre que les… …   Wikipédia en Français

  • Racine carrée de deux — La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu’il est multiplié par lui même, donne le nombre 2, autrement dit √2 × √2 = 2. C’est un nombre irrationnel, dont une valeur approchée à 10 9… …   Wikipédia en Français

  • Racine (Mathématiques) — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes …   Wikipédia en Français

  • Racine N-ième — Racine d un nombre En mathématiques, une racine n ième d un nombre a est un nombre b tel que bn = a, où n est un entier naturel non nul, Selon que l on travaille dans l ensemble des réels positifs, l ensemble des réels ou l ensemble des complexes …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”