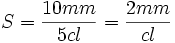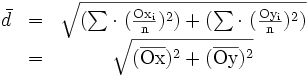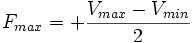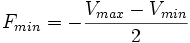Qualite metrologique des appareils de mesure

Qualite metrologique des appareils de mesure

Qualité métrologique des appareils de mesure

La qualité métrologique d'un instrument de mesure ou d'un capteur est l'ensemble des données qui caractérisent la qualité de la mesure effectuée par le dispositif considéré.

Les principales caractéristiques déterminant la qualité d'un appareil sont :

  • L'étendue
  • la résolution
  • la sensibilité
  • l'exactitude
    • la justesse
    • la fidélité

Sommaire

L'étendue de mesure

C'est le domaine de variation possible de la grandeur à mesurer. Elle est définie par une valeur minimale et une valeur maximale. Ces deux valeurs extrèmes s'appellent la portée minimale et la portée maximale.

Exemple :

Un voltmètre aura une étendue de mesure comprise entre 1 volt et 10 volts.

La résolution

La résolution d'un appareil est la plus petite variation de mesure qu'il peut déceler.

On l'exprime souvent en points (ou chiffres), c'est à dire le nombre de valeurs différentes qu'un instrument peut afficher.

Par exemple un multimètre de 2000 points pour un calibre de 2V peut afficher toutes les valeurs comprises entre 0.000 V et 1.999 V ce qui lui donne une résolution de 1 mV.

On rencontre également une autre notation. Au lieu de dire 2000 points on dit 3 point 1/2. L'instrument pourra ainsi afficher toutes les mesures comportant jusqu'à 3 digits compris entre 0 et 9 plus un demi chiffre repésenté par un 1 ou un blanc en tête de la valeur.

La sensibilité

Cas général

La sensibilité est un paramètre exprimant la variation du signal de sortie d'un appareil de mesure en fonction de la variation du signal d'entrée.

Un appareil est d'autant plus sensible qu'une petite variation de la grandeur G à mesurer provoquera un changement plus grand de l'appareil de mesure.

Nota : si la valeur d'entrée est de même nature que la valeur de sortie, la sensibilité est appelée gain.

La sensibilité au voisinage d'une valeur donnée de la grandeur G à mesurer s'exprime de la manière suivante :

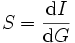S=\frac{{\rm d}I}{{\rm d}G} [1]
I: Indication donnée par l'essai
G: Quantité de grandeur à mesurer

On considère généralement qu'il s'agit de la pente de la courbe de graduation sur un intervalle : la sensibilité moyenne.

On peut écrire alors :

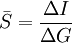\bar S=\frac{\Delta I}{\Delta G} [2]

Exemple :

L'échelon d'un volucompteur est de 1 cm et la valeur d'échelon est de 5 cl.

S=\frac{10 mm}{5 cl}=\frac{2 mm}{cl}

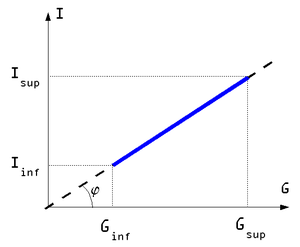
Cas d'un appareil linéaire

La formule [2] n'a de sens que si sur cet intervalle de mesure l'appareil est linéaire. C’est-à-dire si la sortie est proportionnelle à l'entrée.

Sensibilite theorique.png
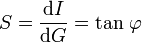S=\frac{{\rm d}I}{{\rm d}G}=\operatorname{tan} \ \varphi [3] ou encore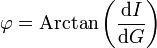 \varphi = \operatorname{Arctan} \left( \frac{{\rm d}I}{{\rm d}G} \right)

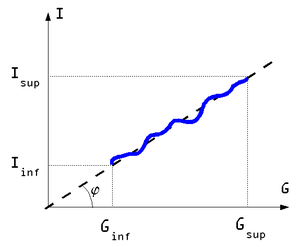
En pratique, on réalise une courbe d'étalonnage où la linéarité est approchée. Pour déterminer la droite on peut utiliser la méthode des moindres carrés.

Il faut préciser que géneralement une pente (d'une dépendance linéaire entre deux grandeurs physiques) a sa propre unité de mesure. Prenons comme premier exemple la dépendance entre l'intensité du courant dans un circuit électrique simple (contenant une source de tension continue et une résistance) en fonction de la tension. Dans ce cas la pente de la droite 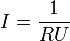I=\frac{1}{RU} a la dimension de l'inverse d'une résistance électrique. 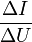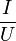Et cette pente est calculée à partir de la formule \frac{\Delta I}{\Delta U}, ou \frac{I}{U} (point U,I pris sur la droite) car la droite doit passer par l'origine du système de coordonnées. Il ne faut pas confondre la pente de la droite physique (ou logique) et la pente de la droite dessinée, qui dépend des échelles utilisées.

Prenons un autre exemple : la détermination de la constante de Planck a partir de l'effet photoélectrique faite par Millikan: en fonction de la fréquence du rayonnement monochromatique qui produit l'effet photoélectrique externe on détermine la tension électrique de freinage qui arrête les photoélectrons. La loi de conservation de l'énergie pour ce processus s'écrit : hν = Eext + eU ou h est la constante de Planck, ν la fréquence du rayonnement monochromatique, Eext le travail d'extraction (des électrons du matériau), e est la charge des électrons et U la tension de freinage qui arrête les photoélectrons. La représentation U(ν) c'est a dire 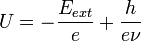U=-\frac{E_{ext}}{e}+\frac{h}{e\nu} donne une droite dont la pente théorique est \frac{h}{e}; la pente expérimentale reste obtenue à partir de la droite tracée, par 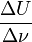\frac{\Delta U}{\Delta\nu}. Finalement on égale les deux pentes, théorique et expérimentale, on connait la valeur de la charge de l'électron et on obtient la valeur de la constante de Planck.

Pour des métaux et pour la lumière visible on a des fréquences de l'ordre de 1014 Hz et des tensions de l'ordre du Volt, ce qui donne des pentes physiques de l'ordre de 10 − 15 V/Hz ou 10 − 15 V.s. La valeur numérique, de 10 − 15, est proche de zéro, ce qui conduirait fausement a l'idée que "l'angle", si on considère la signification fausse de la pente physique comme la tangente d'un angle sur le graphique, est presque nul. On a omis déliberement l'unité de mesure pour la pente dans ce raisonnement, mais normalement on ne doit jamais le faire. En plus, en ce qui concerne la représentation graphique, les meilleurs resultats expérimentaux sont obtenus quand la pente visuelle est proche de 45 degrés, c'est a dire qu'on choisit correctement les échelles verticale et horizontale.

Sensibilite experimentale.png

Sensibilité et résolution

Ne pas confondre la sensibilité avec la résolution (ou pouvoir de résolution).

La résolution est le plus petit écart entre deux valeurs, tel que l'appareil en donne une mesure différente

Exemple :

Un voltmètre indique 100 volts. Une variation de 0,1 volt fait bouger l'aiguille du voltmètre alors qu'une variation de 0,05 volt ne fait pas bouger l'aiguille. La résolution du voltmètre est de 0,1 volt et la sensibilité de 0,05.

L'exactitude de mesure

Un instrument de mesure est d'autant plus exact que les résultats de mesure qu'il indique coïncident avec la valeur vraie (par définition théorique) que l'on cherche à mesurer.

L'exactitude est plus aisée à définir par l'erreur de mesure. Elle s'exprime en unité de grandeur (erreur absolue) ou en pourcentage (erreur relative).

En dehors des conditions opératoires, l'exactitude d'un appareil est essentiellement lié à deux types de caractéristiques : la justesse et la fidélité. Un appareil est exact s'il est à la fois juste et fidèle.

L'exactitude d'un appareil de mesure peut également être entachée par des causes extérieures : erreur opératoire, erreur provoquée par les grandeurs d'influences (température, pression etc), erreur de référence ou d'étalonnage, erreur d'hystérésis, erreur de finesse etc.

La justesse

L'erreur de justesse est l'erreur globale résultant de toutes les causes pour chacun des résultats de mesure pris isolément. C'est donc l'aptitude de l'appareil à donner des résultats qui ne sont pas entachés d'erreur.

Dans le cas de mesures multiples c'est l'écart entre le résultat moyen et la valeur vraie.

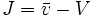
J= \bar v - V
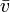\bar v: Moyenne arithmétique d'un grand nombre de mesures
V: Valeur vraie (ou conventionellement vraie)

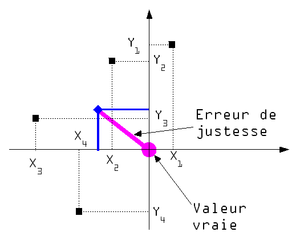
Si l'on effectue une représentation en deux dimensions en considérant la valeur vraie comme l'origine on peut considérer l'erreur de justesse comme le barycentre de l'ensemble des mesures.

représentation dans un espace en deux dimensions de la justesse
\begin{matrix} & \bar d & = & \sqrt{{\rm (\sum \cdot \ ( \frac{Ox_i}{n} )^2)} + {\rm (\sum \cdot \ ( \frac{Oy_i}{n} )^2)} {\rm }} \\ & & = & \sqrt{{\rm ( {\overline {Ox}})^2} + {\rm ( {\overline {Oy}})^2}} \end{matrix}

La fidélité

Définition : La fidélité est l'aptitude d'un appareil de mesure à donner des mesures exemptes d'erreurs accidentelles.

La fidélité définit la dispersion des résultats. Si on n'effectue qu'une seule mesure, la fidélité représente la probabilité qu'elle soit représentative du résultat moyen. Ce dernier aurait été obtenu en effectuant une infinité de mesures.

Nota : le résultat moyen étant lui-même entaché de l'erreur de justesse.

Si on effectue un ensemble de mesures d'une grandeur G, on obtient une valeur maximum (Vmax) et une valeur minimum (Vmin). Les erreurs limites de fidélité sont alors :

F_{max}=+\frac{V_{max}-V_{min}}{2}
F_{min}=-\frac{V_{max}-V_{min}}{2}

Exemple :

Des mesures répétées à l'aide d'un voltmètre donnent

Umax = 100,2V
Umin = 99,7V
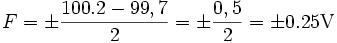
F = \pm \frac {100.2-99,7}{2} = \pm \frac{0,5}{2} = \pm 0.25 {\rm V}

Conclusion

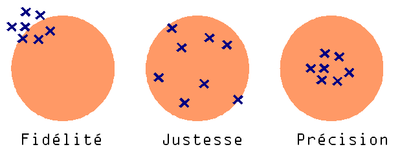
On peut représenter symboliquement la fidélité, la justesse et la précision de la manière suivante :

représentation symbolique de la fidélité, la justesse et la précision en métrologie

Voir également

Normes

Normes internationales (ISO)

  • ISO 5725-1 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 1 : principes généraux et définitions.
  • ISO 5725-2 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 2 : méthode de base pour la détermination de la répétabilité et de la reproductibilité d'une méthode de mesure normalisée.
  • ISO 5725-3 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 3 : mesures intermédiaires de la fidélité d'une méthode de mesure normalisée.
  • ISO 5725-4 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 4 : méthodes de base pour la détermination de la justesse d'une méthode de mesure normalisée.
  • ISO 5725-5 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure - Partie 5 : méthodes alternatives pour la détermination de la fidélité d'une méthode de mesure normalisée
  • ISO 5725-6 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 6 : utilisation dans la pratique des valeurs d'exactitude.
  • ISO/TR 22971 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure - Lignes directrices pratiques pour l'utilisation de l'ISO 5725-2:1994 pour la conception, la mise en œuvre et l'analyse statistique des résultats de répétabilité et de reproductibilité interlaboratoires

Bibliographie

  • Jean-Claude Engrand – De la métrologie fondamentale à son application industrielle – Éditeur Librairie scientifique Albert Blanchart – 1976
  • Jean Perdijon – La mesure science et philosophie – Collection Domino – Éditeur Flammarion – 1998 (ISBN 2-08-035580-5)
  • A.Defix – Élément de métrologie générale et de métrologie légale – École nationale supérieure du pétrole et des moteurs – Édition Technip -1985 (2e édition) (ISBN 2-7108-0496-4)
Ce document provient de « Qualit%C3%A9 m%C3%A9trologique des appareils de mesure ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Qualite metrologique des appareils de mesure de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Qualité métrologique des appareils de mesure — La qualité métrologique d un instrument de mesure ou d un capteur est l ensemble des données qui caractérisent la qualité de la mesure effectuée par le dispositif considéré. Les principales caractéristiques des instruments de mesure (ou… …   Wikipédia en Français

  • Controle de qualite — Contrôle qualité Pour les articles homonymes, voir Contrôle. Le contrôle qualité est un aspect de la gestion de la qualité. Le contrôle est une opération destinée à déterminer, avec des moyens appropriés, si le produit (y compris, services,… …   Wikipédia en Français

  • Contrôle De Qualité — Contrôle qualité Pour les articles homonymes, voir Contrôle. Le contrôle qualité est un aspect de la gestion de la qualité. Le contrôle est une opération destinée à déterminer, avec des moyens appropriés, si le produit (y compris, services,… …   Wikipédia en Français

  • Contrôle de la qualité — Contrôle qualité Pour les articles homonymes, voir Contrôle. Le contrôle qualité est un aspect de la gestion de la qualité. Le contrôle est une opération destinée à déterminer, avec des moyens appropriés, si le produit (y compris, services,… …   Wikipédia en Français

  • Contrôle de qualité — Contrôle qualité Pour les articles homonymes, voir Contrôle. Le contrôle qualité est un aspect de la gestion de la qualité. Le contrôle est une opération destinée à déterminer, avec des moyens appropriés, si le produit (y compris, services,… …   Wikipédia en Français

  • Contrôle qualité — Pour les articles homonymes, voir Contrôle. Le contrôle qualité est un aspect de la gestion de la qualité. Le contrôle est une opération destinée à déterminer, avec des moyens appropriés, si le produit (y compris, services, documents, code… …   Wikipédia en Français

  • Erreur de mesure — Erreur (métrologie) Pour les articles homonymes, voir Erreur et Incertitude. Le calcul d erreur, ou calcul d incertitudes est un ensemble de techniques permettant d estimer l erreur faite sur un résultat numérique, à partir des incertitudes ou… …   Wikipédia en Français

  • Appareil de mesure — Instrument de mesure Le Capitaine Nemo et le Professeur Aronnax contemplant des instruments de mesure dans Vingt mille lieues sous les mers En physique et en sciences de l’ingénieur, mesurer consiste à comparer une grandeur physique qui… …   Wikipédia en Français

  • Instrument De Mesure — Le Capitaine Nemo et le Professeur Aronnax contemplant des instruments de mesure dans Vingt mille lieues sous les mers En physique et en sciences de l’ingénieur, mesurer consiste à comparer une grandeur physique qui caractérise un objet (ou un… …   Wikipédia en Français

  • Instrument de mesure — Le Capitaine Nemo et le Professeur Aronnax contemplant des instruments de mesure dans Vingt mille lieues sous les mers En physique et en sciences de l’ingénieur, mesurer consiste à comparer une grandeur physique qui caractérise un objet (ou un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”