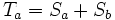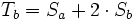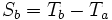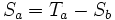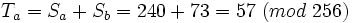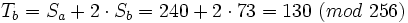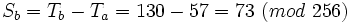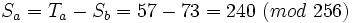Pseudo-transformation de hadamard
- Pseudo-transformation de hadamard
-
Pseudo-transformation de Hadamard
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Pseudo-transformation de hadamard de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Pseudo-transformation de Hadamard — La pseudo transformation de Hadamard est une application de la transformée de Hadamard inventée par le mathématicien français Jacques Hadamard. Elle est utilisée en cryptographie pour ses propriétés de diffusion. Elle est réversible et assure une … Wikipédia en Français
Transformation de Hadamard-Walsh — Transformée de Hadamard La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français… … Wikipédia en Français
Hadamard — Jacques Hadamard Jacques Hadamard Jacques Salomon Hadamard Naissance 8 décembre 1865 Versailles (France) Décès 17& … Wikipédia en Français
Transformee de Hadamard — Transformée de Hadamard La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français… … Wikipédia en Français
Transformée de hadamard — La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français Jacques Hadamard et… … Wikipédia en Français
Transformée de Hadamard — La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français Jacques Hadamard et… … Wikipédia en Français
Jacques-Salomon Hadamard — Jacques Hadamard Jacques Hadamard Jacques Salomon Hadamard Naissance 8 décembre 1865 Versailles (France) Décès 17& … Wikipédia en Français
Jacques Hadamard — Jacques Salomon Hadamard Naissance 8 décembre 1865 Versailles (France) Décès 17 octobre 1963 … Wikipédia en Français
Hadamard transform — The Hadamard transform (also known as the Walsh Hadamard transform, Hadamard Rademacher Walsh transform, Walsh transform, or Walsh Fourier transform) is an example of a generalized class of Fourier transforms. It is named for the French… … Wikipedia
Pseudo-Hadamard transform — The pseudo Hadamard transform is a reversible transformation of a bit string that provides cryptographic diffusion. See Hadamard transform.The bit string must be of even length, so it can be split into two bit strings a and b of equal lengths,… … Wikipedia
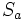 et
et 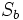 de taille n/2. Pour calculer la transformation
de taille n/2. Pour calculer la transformation 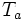 et
et 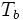 , on utilise les équations suivantes (en modulo 2n) :
, on utilise les équations suivantes (en modulo 2n) :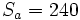 et
et 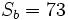 , nous effectuons une substitution modulo 256 ce qui serait le cas si nous travaillions avec des octets dans une procédure de chiffrement :
, nous effectuons une substitution modulo 256 ce qui serait le cas si nous travaillions avec des octets dans une procédure de chiffrement :