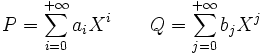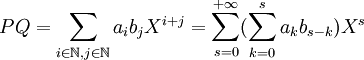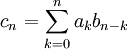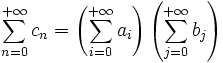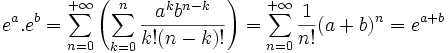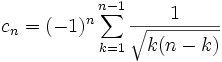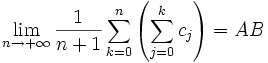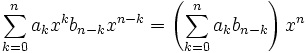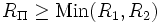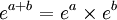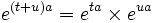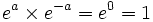Produit de cauchy

Produit de cauchy

Produit de Cauchy

Page d'aide sur l'homonymie Pour les articles homonymes, voir Cauchy.

En analyse, le produit de Cauchy est une opération portant sur certaines séries. Il permet de généraliser la propriété de distributivité. Son nom est un hommage à l'analyste français Augustin Louis Cauchy. Il s'agit d'un produit de convolution discret.

Sommaire

Préliminaire : une écriture du produit de polynômes

Une écriture particulière des coefficients du produit de polynômes permet de comprendre l'introduction de la formule du produit de Cauchy. Soient deux polynômes à coefficients complexes P et Q donnés par leur décomposition dans la base canonique

P=\sum_{i=0}^{+\infty} a_i X^i \qquad Q=\sum_{j=0}^{+\infty} b_j X^j

où les coefficients de P et de Q sont nuls à partir d'un certain rang. Alors leur produit se décompose comme

PQ=\sum_{i\in \N, j\in \N} a_i b_j X^{i+j}=\sum_{s=0}^{+\infty} (\sum_{k=0}^s a_k b_{s-k}) X^s

La réindexation nécessaire ne pose pas de difficulté puisque la somme est en fait finie.

Produit de Cauchy de séries complexes

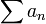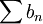Le produit de Cauchy des séries \sum a_n et \sum b_n de nombres complexes est la série de terme général

c_n=\sum_{k=0}^n a_k b_{n-k}

Sous des hypothèses convenables, cette série convergera, et on pourra écrire la formule de distributivité généralisée

\sum_{n=0}^{+\infty} c_n=\left(\sum_{i=0}^{+\infty} a_i\right) \left(\sum_{j=0}^{+\infty} b_j\right)

Si les séries sont toutes les deux à termes nuls à partir d'un certain rang, il suffit d'utiliser le résultat du paragraphe précédent dans le cas X=1. Mais en général, il n'est pas possible d'affirmer que la propriété est vraie puisqu'on ne peut pas réindexer de façon arbitraire des sommes de séries (voir famille sommable pour une justification).

Cas de deux séries absolument convergentes

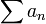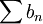Lorsque les séries \sum a_n et \sum b_n sont toutes deux absolument convergentes, leur produit de Cauchy converge et la formule de distributivité généralisée est vérifiée. Il suffit en effet d'utiliser les propriété de commutativité et d'associativité des familles sommables.

Notamment, pour deux complexes a et b, on peut faire le produit de Cauchy des séries définissant l'exponentielle

e^a . e^b = \sum_{n=0}^{+\infty} \left(\sum_{k=0}^n \frac{a^kb^{n-k}}{k!(n-k)!}\right) =\sum_{n=0}^{+\infty} \frac1{n!} (a+b)^n = e^{a+b}

À partir de cette propriété, il est possible également de définir le produit de Cauchy de deux séries entières, dont les propriétés sont étudiées ci-après.

Théorème de Mertens

Le mathématicien allemand Franz Mertens a prouvé une propriété de convergence plus forte : si une des deux séries converge et l'autre converge absolument, alors leur produit de Cauchy converge et la formule de distributivité généralisée a bien lieu.

En revanche, si on suppose seulement que les deux séries convergent, on n'est pas assuré que la série produit de Cauchy converge. Ainsi si on considère la série de terme général 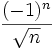\frac{(-1)^n}{\sqrt n}, et qu'on forme son produit de Cauchy avec elle-même, on obtient pour terme général

c_n = (-1)^n \sum_{k=1}^{n-1} \frac1{\sqrt{k(n-k)}}

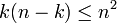Or k(n-k) \le n^2 de sorte que 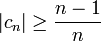\left|c_n\right| \ge {n-1 \over n} et que ce terme ne tend pas vers 0, entraînant la divergence grossière de la série.

Théorèmes de convergence

Si deux séries convergent il y a pourtant des résultats de convergence positifs pour leur produit de Cauchy. En reprenant les notations 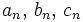a_n,\, b_n,\, c_n pour les termes généraux des deux séries et de la série produit de Cauchy, et en notant A et B les sommes des deux premières séries

  • si la série produit 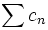\sum c_n converge, alors ce ne peut être que vers le produit AB, c'est une conséquence du théorème d'Abel
\lim\limits_{n\to +\infty}\frac1{n+1} \sum_{k=0}^n \left(\sum_{j=0}^k c_j\right) = AB

Produit de Cauchy de séries entières

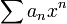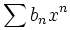Deux séries entières \sum a_n x^n et \sum b_n x^n étant données, leur produit de Cauchy est également une série entière, puisque le terme général vaut

\sum_{k=0}^n a_k x^k b_{n-k} x^{n-k}= \left(\sum_{k=0}^n a_k b_{n-k}\right) x^n

En notant R1,R2 les rayons de convergence respectifs des deux séries entières, le rayon de convergence RΠ de la série produit vérifie l'inégalité

R_\Pi \geq \mathrm{Min }(R_1,R_2)

En effet, si on considère un complexe de module strictement inférieur à ce minimum, les deux séries entières convergent absolument, la série produit aussi, et sa fonction somme est le produit des fonctions sommes des deux séries. On en déduit que le produit de deux fonctions développables en série entière sur un ouvert est lui aussi développable en série entière.

L'inégalité précédente peut être stricte. C'est le cas par exemple si on prend pour les deux séries 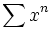\sum x^n (rayon 1) d'une part et 1 − x d'autre part (rayon infini). La série produit est réduite à 1 et a un rayon de convergence infini.

Plus surprenant, le rayon de la série produit peut être infini alors même que les deux rayons des séries initiales sont finis. Par exemple si on considère le développement de 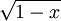\sqrt{1-x} en série entière, le rayon de convergence est 1. Mais quand on fait le produit de Cauchy de cette série avec elle-même, on obtient la série 1 − x, donc un polynôme de rayon infini.

Généralisation aux algèbres de Banach

On suppose que A est une algèbre de Banach. Alors il est possible de définir la notion de produit de Cauchy de deux séries à valeurs dans A. En outre, le produit de Cauchy de deux séries absolument convergentes converge, et la formule de distributivité généralisée tient toujours.

Par exemple, il est possible de reprendre le calcul du produit de deux exponentielles effectué dans le cas complexe. La seule propriété qui manque pour pouvoir écrire la formule est la possibilité d'appliquer la formule du binôme de Newton, ce qui demande de supposer par exemple que a et b commutent. Sous cette hypothèse

e^{a+b}=e^a\times e^b

Par exemple, si t,u sont des scalaires on a toujours

e^{(t+u)a}=e^{ta}\times e^{ua}

Une autre formule importante : si b=-a,

e^a\times e^{-a}=e^0=1
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Produit de Cauchy ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Produit de cauchy de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Produit de Cauchy — Pour les articles homonymes, voir Cauchy. En analyse, le produit de Cauchy est une opération portant sur certaines séries. Il permet de généraliser la propriété de distributivité. Son nom est un hommage à l analyste français Augustin Louis Cauchy …   Wikipédia en Français

  • Cauchy — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.  Cette page d’homonymie répertorie des personnes (réelles ou fictives) partageant un même patronyme. Patronyme Augustin Louis Cauchy (1789 1857),… …   Wikipédia en Français

  • CAUCHY (A.-L.) — Moins profond et moins universel que Gauss, Dirichlet, Abel ou Galois, Cauchy a cependant été le maître incontesté de l’analyse dans la première moitié du XIXe siècle, et son œuvre a marqué un tournant dans l’histoire des mathématiques. Un… …   Encyclopédie Universelle

  • Cauchy-Schwarz — Inégalité de Cauchy Schwarz Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de… …   Wikipédia en Français

  • Produit scalaire — En géométrie vectorielle, le produit scalaire est une opération algébrique s ajoutant aux lois s appliquant aux vecteurs. À deux vecteurs elle associe leur produit, qui est un nombre réel (ou scalaire). Elle permet d exploiter les notions de la… …   Wikipédia en Français

  • Produit scalaire hermitien — Hermitien Plusieurs entités mathématiques sont qualifiées d hermitiennes en référence au mathématicien Charles Hermite. Sommaire 1 Espace hermitien 2 Produit scalaire hermitien 3 Opérateur hermitien …   Wikipédia en Français

  • Produit hermitien — Hermitien Plusieurs entités mathématiques sont qualifiées d hermitiennes en référence au mathématicien Charles Hermite. Sommaire 1 Espace hermitien 2 Produit scalaire hermitien 3 Opérateur hermitien …   Wikipédia en Français

  • Inégalité de Cauchy-Schwarz — Pour les articles homonymes, voir Cauchy et Schwarz.  Ne doit pas être confondu avec Inégalité de Cauchy. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1 …   Wikipédia en Français

  • Augustin Louis Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy Cauchy vers 1840. Lithographie de Zéphirin Belliard d après une peinture de Jean Roller …   Wikipédia en Français

  • Augustin-Louis Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”