Problème de Fagnano

Le problème de Fagnano, encore appelé problème du triangle de Schwarz, est un célèbre problème de géométrie euclidienne énoncé par le mathématicien italien Giulio Fagnano (it) (1682-1766) : Peut-on inscrire un triangle de périmètre minimal dans un triangle acutangle donné ?

Énoncé

Démonstration

Soit ABC le triangle donné. Nous voulons trouver les points M, N et P sur les côtés [BC], [AC] et [AB] respectivement, de sorte que le périmètre de ΔMNP soit minimal.

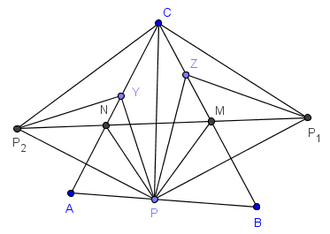
Premièrement, nous considérons une version plus simple du problème. Fixons un point P arbitraire sur (AB). Nous allons maintenant trouver les points M et N sur (BC) et (AC) respectivement, de sorte que ΔMNP soit de périmètre minimal (bien entendu, le minimum dépendra du choix de P). Soit P₁ l'image de P par la réflexion d'axe (BC) et P₂ d'axe (AC). Alors CP₁ = CP = CP₂, et . En posant , nous avons alors . De plus, 2γ < 180, puisque γ < 90 par définition. Par conséquent, (P₁P₂) coupe les côtés [BC] et [AC] de ΔABC aux points M et N respectivement et le périmètre de ΔMNP est égal à P₁P₂. D'une manière analogue, si Z est un point quelconque sur [BC] et Y un point quelconque sur [AC], le périmètre de ΔZPY est égal à la longueur de la ligne brisée P₁ZYP₂, qui est plus grande ou égale à P₁P₂. Ainsi, le périmètre de ΔPZY est plus grand ou égal au périmètre de ΔPMN et l'égalité a lieu précisément lorsque Z = M et Y = N.

Ainsi, nous devons trouver un point P de [AB] de sorte que [P₁P₂] soit de longueur minimal. Remarquons que ce segment est la base d'un triangle isocèle P₂P₁C avec comme angle constant 2γ au point C et comme côtés CP₁ = CP₂ = CP. Ainsi, nous devons choisir P sur [AB] de sorte que CP₁ = CP soit minimal. Il est évident que ce minimum est obtenu lorsque P est le pied de la hauteur issue de C.

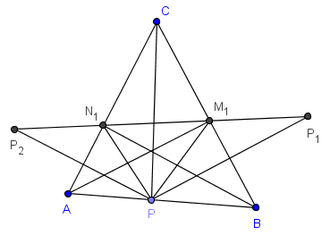
Remarquons maintenant que si P est le pied de la hauteur issue de C, alors M et N sont les pieds des deux autres hauteurs de ΔABC. Pour prouver cette assertion, notons M₁ et N₁ les pieds des hauteurs de ΔABC passant par A et B respectivement. Alors

ce qui montre que le point P₁ appartient à la droite (M₁N₁). D'une manière analogue, P₂ appartient à la droite (M₁N₁) et donc M = M₁ et N = N₁.

En conclusion, de tous les triangles inscrits à ΔABC, celui ayant ses sommets confondus avec les pieds des hauteurs issues de ΔABC a son périmètre qui est minimal.

Cas du triangle obtusangle

Lorsque ΔABC est obtusangle, le triangle MNP est tel que M = N = C et P le pied de la hauteur issue de C. Dans ce cas, on dit que ΔMNP est dégénéré.

• Portail de la géométrie