- Portée d'un missile
-
Portée (balistique)
La portée d'un projectile correspond à la longueur entre la projection horizontale du point où le projectile est lâché par le système lui donnant son impulsion, et la projection horizontale du point de chute du projectile. La portée est donc la projection horizontale d'une trajectoire courbe en trois dimensions.
Sommaire
À la surface de la Terre
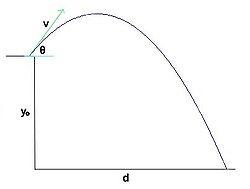
En physique, le cas le plus courant est celui d'un projectile qui suit une trajectoire du type parabolique, déterminée par des conditions initiales strictes dans un champ de gravité uniforme — c'est-à-dire le cas de figure rencontré à la surface de la Terre. Pour des longueurs raisonnables, la surface de la Terre est approximée en un plan de nature horizontale qui fournit l'axe orienté sur lequel sera mesurée la portée.
Avec les paramètres suivants :
- g : l'accélération gravitationnelle (valeur approchée de 9.81 m/s2 à la surface de la Terre) ;
- θ : l'angle de projection par rapport à l'horizontale ;
- v : la vitesse de déplacement initiale (vélocité) du projectile ;
- y0 : la hauteur initiale du projectile par rapport à l'horizontale, niveau zéro en hauteur ;
- d : la distance horizontale totale parcourue par le projectile, ou portée ;
et en négligeant les frottements de l'air :
Si y0 est prise comme valant 0 — c'est-à-dire que le projectile est lancé à partir de l'horizontale de niveau 0 (ie. le sol, typiquement) — le calcul se simplifie en :
Preuves
Cas où y0 vaut 0
La position du projectile est caractérisé par deux équations de mouvement, selon les axes horizontaux et verticaux.
La position horizontale du projectile, x(t), est :
Dans la direction verticale, où s'applique la force de pesanteur, elle vaut :
Le point de chute et d'arrêt de la trajectoire correspond au retour du projectile à la position verticale initiale — ici, 0 :
Par résolution d'une équation du second degré, deux solutions existent :
ou bien
La première solution correspond à la position initiale. C'est donc la seconde solution qui permet de déterminer la portée. En introduisant t dans l'équation modélisant la position horizontale, il vient que :
Par application de l'identité trigonométrique :
on peut simplifier la solution en :
À noter que pour un angle de projection θ égal à 45°, la solution devient :
On parle alors de « portée maximale » : c'est la raison pour laquelle les lanceurs de javelots, par exemple, s'entraînent à former ce demi-angle droit pour maximiser la distance parcourue.
Cas général
Si y0 peut être non nul, les équations de mouvement deviennent :
et
En résolvant encore une fois pour t avec la position y égale à 0, il vient :
La résolution de l'équation du second degré donne toujours deux solutions en temps. Après plusieurs manipulations algébriques :
La racine carré doit être positive, et puisque la vélocité et le cosinus de l'angle de projection sont supposés l'être également, la solution avec le plus grand temps sera celle correspondant au plus affectant le dernier membre de droite. De ce fait, la solution générale est de la forme :
La portée est donc :
Références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Range of a projectile ».
Voir aussi
- Portail de la physique
Catégories : Mesure de longueur | Mécanique
Wikimedia Foundation. 2010.

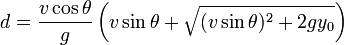
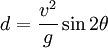
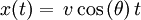
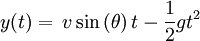
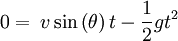
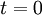
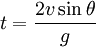
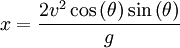
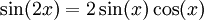
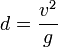
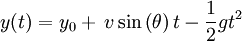
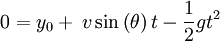
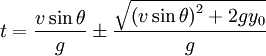
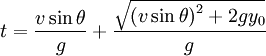
![d = \frac {v \cos \theta} {g} \left [ v \sin \theta + \sqrt{\left(v \sin \theta \right)^2 + 2 g y_0} \right]](/pictures/frwiki/102/f53a1edde08b3c1c131c0498ea87f8a4.png)