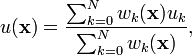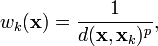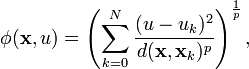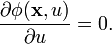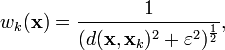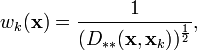- Pondération Inverse à la Distance
-
Pondération Inverse à la Distance
(Traduction de la version anglaise)
La Pondération Inverse à la Distance (PID) est une méthode d'interpolation spatiale, un processus permettant d'assigner une valeur à un espace non connu à partir d'un semis de points connus.
Une forme courante pour trouver une valeur interpolée u à partir d'un point donné x en utilisant la PID est une fonction d'interpolation :
où :
est une fonction simple de pondération, comme définie par Shepard[1], x étant un point (théorique) interpolé, xk est un point interpolé (connu), d est une distance donnée (opérateur de mesure) du point connu xk au point inconnu x, N est le nombre total de points connus utilisés dans l'interpolation et p est un nombre positif réel, appelé le paramètre de puissance. Ici, le poids des points voisins diminue lorsque la distance augmente. Les plus grandes valeurs de p donnent une influence plus grande aux valeurs les plus proches du point interpolé. Pour 0 < p < 1 u(x) donne des pics lissés au dessus du point interpolé xk, alors que pour p > 1 le pic devient plus pointu. Le choix de p est donc une fonction du degré de lissage désiré pour l'interpolation, de la densité et la distribution des échantillons interpolés, et de la distance maximum au delà de laquelle un échantillon individuel peut influencer les points environnants.
La méthode de Shepard est une conséquence de la minimalisation d'une fonction liée à la mesure des déviation entre les tuples de points interpolés {x, u} et k tuples de points interpolés {xk, uk}, définis comme :
dérivé de la condition de minimalisation :
La méthode peut être aisément étendue à des dimensions supérieures de l'espace et est en fait une généralisation de l'approximation de Lagrange aux espaces multidimensionnels.
Une version modifiée de l'algorithme créé pour l'interpolation trivariée a été développée par A modified version of the algorithm designed for trivariate interpolation was developed Robert J. Renka et est disponible dans Netlib comme "algorithm 661" dans la bibliothèque "toms" (?).
Sommaire
Méthode de Liszka
Une modification de la méthode de Shephard a été proposée par Liszka[2] [Cette référence doit être vérifiée ! Dans le papier indiqué, la formule n'apparaît pas etle papier parle d'une méthode basée sur l'expansion de Taylor. De plus, à la fin de l'article, dernière ligne de la page 1609 de l'article en question, il est écrit "Aucune forme explicite de la fonction n'est disponible"] en application à la mécanique expérimentale, qui propose d'utiliser :
comme fonction de pondération, où ε est choisi en fonction de l'erreur statistique de mesure des points interpolés.
Mesure de Lukaszyk-Karmowski
Une autre modification de la méthode de Shephard a été proposée par Łukaszyk[3] aussi en application à la mécanique appliquée. La fonction de pondération proposée avait la forme suivante :
où
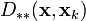 est la mesure de Lukaszyk-Karmowski choisie également vis à vis de l'erreur statistique et la distribution de la probabilité de la mesure des points interpolés.
est la mesure de Lukaszyk-Karmowski choisie également vis à vis de l'erreur statistique et la distribution de la probabilité de la mesure des points interpolés.References
- ↑ Shepard, Donald (1968). "A two-dimensional interpolation function for irregularly-spaced data". Proceedings of the 1968 ACM National Conference: 517–524. DOI:10.1145/800186.810616.
- ↑ T. Liszka, « An interpolation method for an irregular net of nodes », dans International Journal for Numerical Methods in Engineering, vol. 20, no 9, 1984, p. 1599–1612 [lien DOI]
- ↑ *A new concept of probability metric and its applications in approximation of scattered data sets
Voir aussi
- Interpolation spatiale
Ä
Catégories : Mathématiques interdisciplinaires | Interpolation spatiale
Wikimedia Foundation. 2010.